Non Context-Free Languages

Overview

We have seen that context-free languages are more powerful than regular languages. However they have limits; there are many types of languages that are not context free.

We will discuss languages in this category and how we can prove a language is not context-free.

Pumping Lemma for Context-Free Languages

Like regular languages, context-free languages have a pumping lemma which is given below:

If $A$ is a context free language, then there is a number $p$ where, if $s$ is a string in $A$ of length at least $p$, then $s$ may be divided into five pieces $s = uvxyz$ such that:

$\forall i \ge 0, uv^ixy^iz \in A$
$|vy| > 0$
$|vxy| \le p$

Pumping Lemma Explanation

If $A$ is a context-free language, it has some grammar, $G$, which generates it. The grammar $G$ has a finite number of variables, let's call this the number $p$.

If $s$ is some string in $A$, then there is a parse tree of $s$. If the string $s$ is larger than $p$, then some variable $R$ must be repeated in the parse tree (by the pigeon-hole principle).

Because there was some sequence of the derivation that brought us from $R$ back to $R$, then we could repeat that sequence and "pump" $R$ again, and still have a valid parse tree.

We could also remove the portion of the string that repeated $R$ and still have a valid string in $A$:

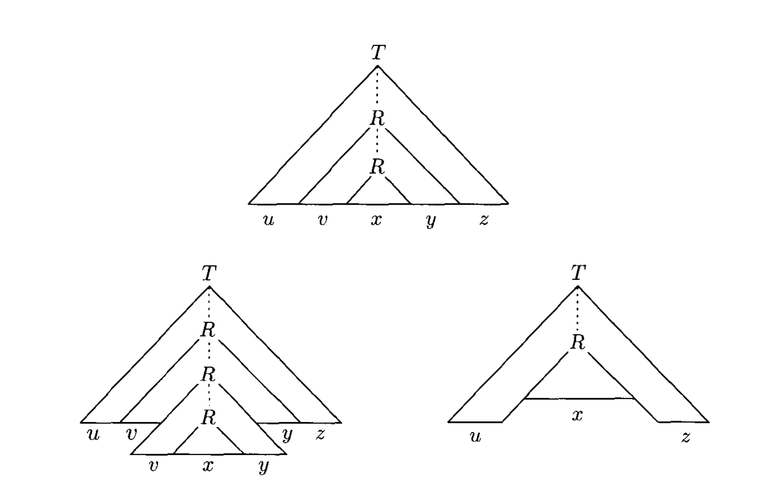
Another way of looking at the pumping lemma for context-free languages is by considering how a grammar can "loop", which is via recursion. A recursive rule can be generalized like this:

$A \rightarrow vAy \ |\ x$

Here, $v$, $y$, and $x$ are strings of terminals (or variables which can reduce to terminals). A recursive rule contains the portion of the string before the recursion ($v$), the portion after the recursion ($y$) and also the base case ($x$).

$u$ and $z$ are the parts leading up to the recursive rule, and following the recursive rule:

$S \rightarrow uAz$

Any context-free grammar which can generate arbitrarily-long strings must have some type of recursive rule like this.

The pumping lemma just says that we can repeat that recursion any number of times we like and still have a string in the language.

Context Free Example

How can we show the pumping lemma holds for $\{0^n1^n | n \ge 0\}$?

Proving A Language is Not Context-Free

To prove that a language is not context-free, we can show that, for some string in the language with at least length $p$, there is no way to divide it such that the pumping lemma holds.