Nondeterministic Finite Automata

Overview

The deterministic part of DFA means that each DFA can only do one particular thing at each step of the computation.

In a nondeterministic finite automata, this is not the case. Several choices of which state to transition to may exist.

Formally, the difference between a DFA and an NFA is that the output from the transition function of a DFA is a single state. The output from the transition function of an NFA is a set of states.

Example

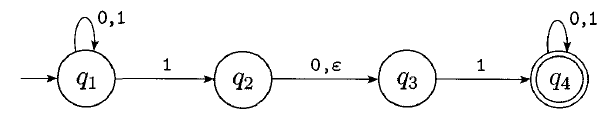
This is an example of an NFA. It violates several rules of DFAs:

There are two choices when in state $q_{1}$ when we read a 1. When there are multiple options, we can choose to take either.
There is no choice when in state $q_3$ when we read a 0.
There is an "$\epsilon$ transition" out of state $q_{2}$. An epsilon transition is one we can choose to take without consuming any input.

An NFA accepts if any possible path will lead us to an accept state for a given input.

Will the above NFA accept:

101
0001
100001
11000
01010101100

How can we describe the language of this NFA?

How NFAs Compute

NFAs can be viewed as parallel machines that spawn a new thread for each choice. As soon any thread reaches an accept state, the computation halts:

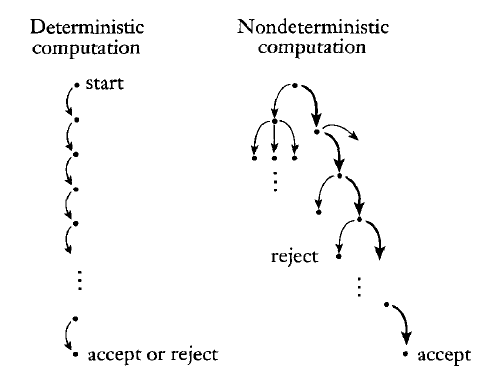
We can thus look at the execution of an NFA as a tree of computation:

NFAs vs. DFAs

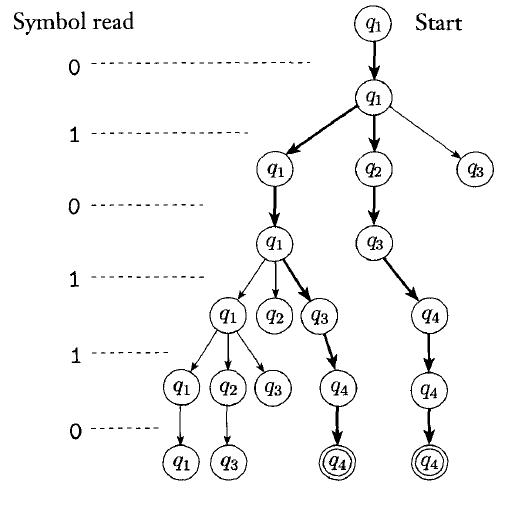
Nondeterminism gives us a lot of flexibility when constructing automata.

The NFA below recognizes the following language:

$\{w | w\text{ contains a 1 in the third position from the end}\}$.

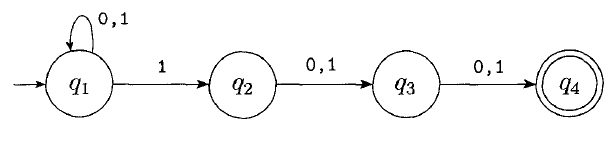
Trace this NFA with inputs to see how it works:

0101111
0100
100
1
1000

It is possible to construct a DFA which recognizes this same language:

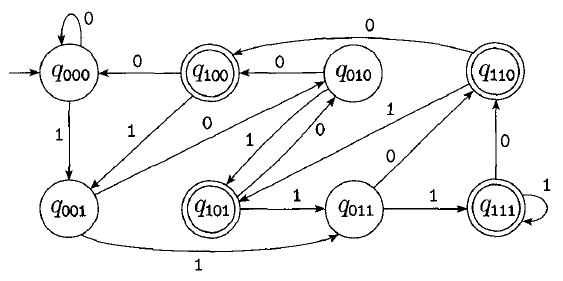
This is the DFA with minimum states recognizing this language.

As we will prove next time, all NFAs have an equivalent DFA. This means that NFAs and DFAs are equivalent in power. To show that a language is regular, you can construct a DFA or NFA which recognizes it.

Closure of Union

We have already shown that regular languages are closed under the union operation. However, this is even easier to show by using non-determinism.

Recall that $A_{1} \cup A_{2} = \{x | x \in A_{1} \text{ or } x \in A_{2}\}$

If $A_{1}$ and $A_{2}$ are both regular, than some machine $N_{1}$ and $N_{2}$ recognize them.

We can easily construct an NFA, N as follows:

Closure of Concatenation

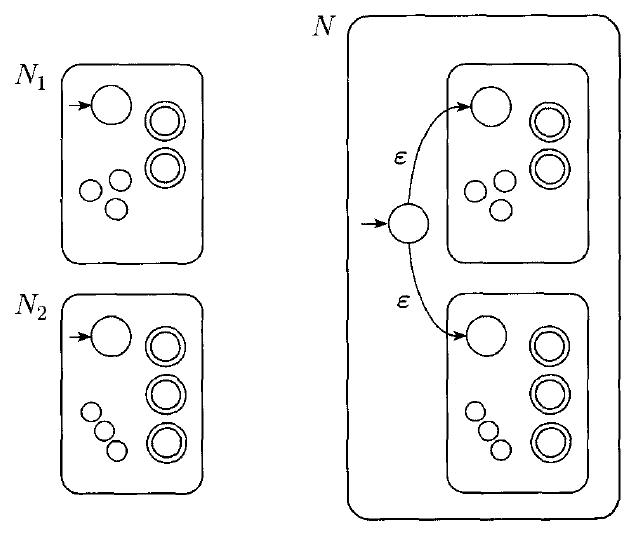
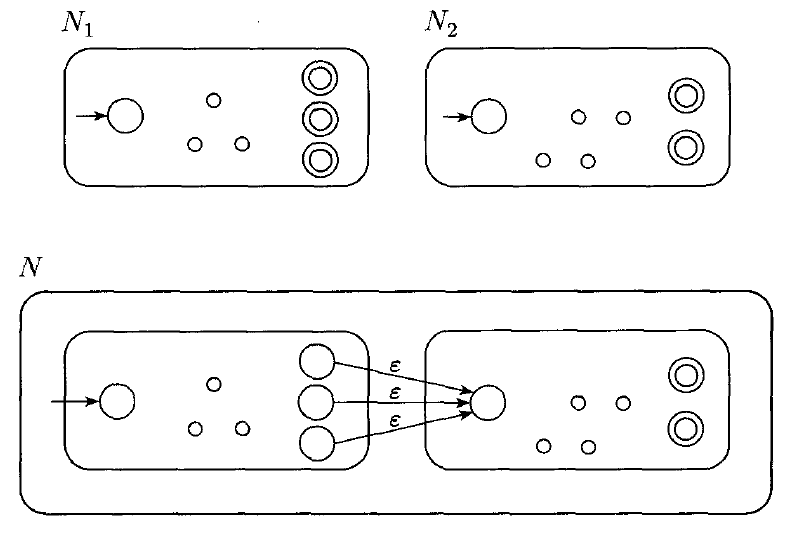
Recall that $A_{1} \circ A_{2} = \{xy | x \in A_{1} \text{ and } y \in A_{2}\}$

Given two NFAs $N_{1}$ and $N_{2}$, we can construct an NFA recognizing the concatenation as follows:

Closure of Star

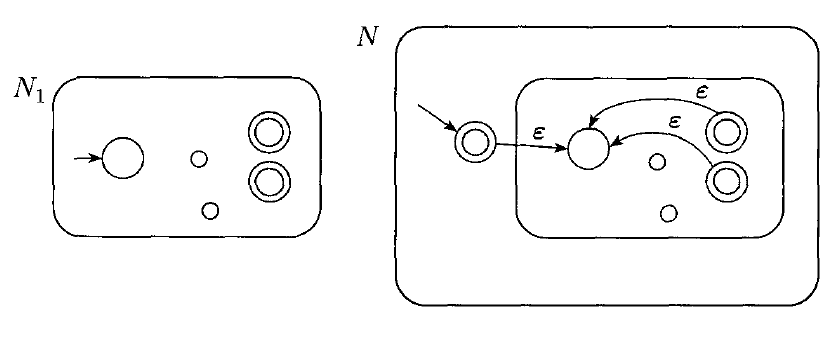
Recall that $A_{1} \ast = \{x_{1}x_{2} ... x_{k} | k \geq 0$ and each $x_{i} \in A_{1}\}$

Given an NFA $N_{1}$ which recognizes $A_{1}$, we can build an NFA which recognizes $A_{1} \ast$ as follows: