Collatz Graphs

September 22, 2015

The Collatz conjecture is one of my favorite things from math. It says that if you take any number and repeatedly divide it by two when even, and multiply by 3 and add one when odd, that you will eventually reach 1. Despite appearing simple, this conjecture has never been proven – though it has been shown to be true for every number tested so far.

In one XKCD comic, the sequence of numbers is drawn as a graph with edges from each number in the sequence to the next. I found several versions of this graph, but wanted to see an even bigger one. So I wrote the following program which generates such a graph for all numbers up to the starting number given. Here is the program code (which uses the awesome graphviz utility for producing the images):


#include <stdio.h>
#include <string.h>
#include <stdlib.h>

/* compute the next number in the Collatz sequence of value */
unsigned collatz(unsigned value) {
    if (value % 2) {
        return 3 * value + 1;
    } else {
        return value / 2;
    }
}

/* a node in the graph */
struct Node {
    unsigned value;
    unsigned next;;
};

/* test if there is a path from node s to node t in the graph */
int find(int s, int t, struct Node* graph, int n) {
    /* if node s IS node t, we've done it */
    if (s == t) {
        return 1;
    }

    /* if node s is bigger than n, then there is no path -
     * well there is one, but we wont' show it! */
    if (s > n) {
        return 0;
    }

    /* if the node is zero, then no path - this can happen
     * when we have already removed the node s would travel
     * trhough from the graph */
    if (s == 0) {
        return 0;
    }

    /* now we recurse on the link from s */
    return find(graph[s].next, t, graph, n);
}


int main(int argc, char** argv) {
    /* check they passed a number */
    if (argc != 2) {
        printf("usage: %s N\n", argv[0]);
        return -1;
    }
    unsigned n = atoi(argv[1]);
    if (n == 0) {
        printf("usage: %s N\n", argv[0]);
        return -1;
    }

    /* an array of nodes (one extra for n itself */
    struct Node graph[n + 1];
    graph[1].value = 1;
    graph[1].next = 0;

    /* for each number we are looking at */
    unsigned i;
    for (i = 2; i <= n; i++) {
        /* create the node for it */
        graph[i].value = i;

        /* compute its next collatz step */
        graph[i].next = collatz(i);
    }

    /* go through the graph and remove ones which don't reach 1, this
     * ensures the graph which is printed is complete */
    for (i = 2; i <= n; i++) {
        if (!find(i, 1, graph, n)) {
            graph[i].value = 0;
            graph[i].next = 0;
        }
    } 

    /* open the file and dump the preamble */
    FILE* f = fopen("collatz.gv", "w");
    fprintf(f, "digraph G {\n");

    /* dump all the nodes */
    for (i = 1; i<= n; i++) {
        /* print the node */
        if (graph[i].value) {
            fprintf(f, "    n%d[label=\"%d\"];\n", graph[i].value, graph[i].value);
        }

        /* print the link */
        if (graph[i].next) {
            fprintf(f, "    n%d -> n%d;\n", graph[i].value, graph[i].next);
        }
    }

    /* dump the postamble and close */
    fprintf(f, "}\n");
    fclose(f);

    /* generate the image */
    system("dot -Tpng collatz.gv -o collatz.png");

    return 0;
}

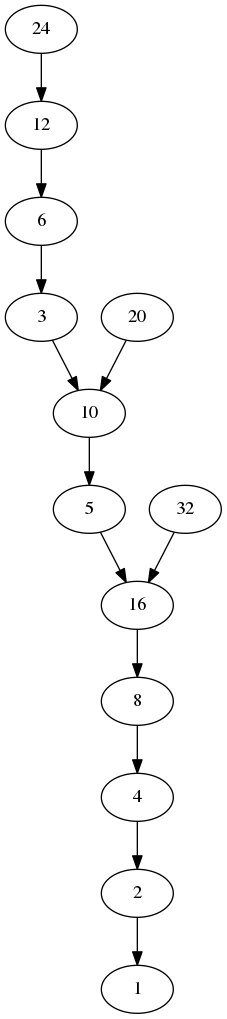
And here is the output for a size of 32 (the program only shows the portion of the graph which actually connects to node 1):

This link shows the very large (2447 * 4763) image for all numbers up to 1,000.