Haskell is a popular functional programming language. Like any functional language, functions are 1st class values and the primary way to write programs.
It is, however, quite different from most other languages:
It's pure
This means that there is no way to update a variable. If a variable is set to a value, that value can never change.
Because of this, Haskell programs have a property called referential transparency which means that any expression can always be replaced with its value without changing the program. This includes function calls which can only depend on their parameters, not any other state.
Benefits of this include making programs easier to reason about and debug, and enabling compiler optimizations.
It's lazy
This means that, unlike most languages, Haskell does not evaluate expressions until they are actually needed. This allows Haskell to do things such as create infinite data structures:
let naturals = [1 ..]
Haskell also features the following:
There are a few Haskell compilers, but the de facto standard one is GHC. GHC includes both a compiler (ghc) and an interpreter (ghci). GHC is installed on the CPSC server.
Hello World in Haskell looks like this:
-- hello world program
main = putStr "Hello World!\n"
This can be compiled as follows:
$ ghc hello.hs
$ ./hello
Hello World!
Haskell programs typically have a .hs extension.
You can also run this in the interpreter as follows:
$ ghci
Prelude> putStr "Hello World!\n"
Hello World!
Prelude>
"Prelude" is the name of the Haskell standard library.
Primitive types in Haskell include:
Int
A native machine integer that could be 32 or 64 bits.
Integer
An arbitrarily large integer type.
Double
A IEEE double-precision value.
Float
A IEEE single-precision value.
Char
A unicode character.
Bool
The value either True or False.
Type names are always capitalized.
The arithmetic and logical operators of Haskell are similar to those of other programming languages. Operators are written infix and include +, -, *, /, <, >, &&, || etc.
Some exceptions are:
Haskell also uses normal precedence and associativity rules.
Functions in Haskell are called differently from most imperative languages. There are no parenthesis around the function or commas. The mod function would be called as:
> mod 105 10
5
It is an error to call functions any other way:
> mod(105, 10) -- error
> mod(105 10) -- error
Functions can be composed together with parenthesis:
> mod (mod 105 10) 2
Functions with exactly two parameters can be called with an infix notation:
> 105 `mod` 10
> (+) 3 5
Haskell has many functions built-in, but the real power is in defining your own functions.
Defining functions uses a simple syntax:
add x y = x + y
The function name is given first, then the parameters, an equal sign, and then the function body.
There is no "return" in Haskell, the body of the function is an expression that the function evaluates to.
Simple Examples:
-- average of three numbers
average a b c = (a + b + c) / 3
-- absolute value
absolute x =
if x < 0 then (-x) else x
Like Racket, if is an expression rather than a statement.
Haskell also supports lambda functions which can be included as part of another expression. The syntax for these is:
\ param1 param2 param3 -> body
For example the add function could also be defined as:
let add = \ a b -> a + b
Like in Racket, lambda functions are most useful for passing into other functions.
Haskell has no loops (and unlike Racket we cannot add loops ourselves since there is no way to update a variable in Haskell). All repetition must be handled via recursion. We can write the factorial function as follows:
fact x =
if x < 2 then 1
else x * fact (x - 1)
This also illustrates the if/else expression in Haskell.
Haskell also allows the piecewise definition of functions, based on a notation taken from mathematics. Here we can define the base cases in separate function lines, using the same function name.
For example, we can define a function to compute the fibonacci number sequence like this:
-- fibonacci sequence
fib 0 = 1
fib 1 = 1
fib x = fib (x - 2) + fib (x - 1)
How can we write a function to compute the sum of the numbers from 1 through a parameter n?
Simple recursion is typically less efficient than iteration and uses more memory. In order to avoid this, Haskell (and many other languages) optimize a case of recursion.
A tail recursive function is one in which the last step of the function is the recursion. The factorial function above is not tail recursive because the recursive call is not the last step.
We can write a tail recursive factorial using an accumulator like so:
fact x accumulator =
if x < 2 then accumulator
else fact (x - 1) (accumulator * x)
This is equivalent to the traditional iterative version where we keep track of the current factorial (accumulator) and a counter (x).
To avoid passing the accumulator for the first call, we can use a separate (nested) function:
fact x =
fact' x accumulator =
if x < 2 then accumulator
else fact (x - 1) (accumulator * x)
fact' x 1
We can write a tail-recursive fibonacci function as:
-- helper function
fib' a b accum i x =
if x == 0 then 1
else if x == 1 then 1
else if i == x then accum
else (fib' b (a + b) (a + b) (i + 1) x)
-- calculate the xth fibonacci number
fib x =
fib' 0 1 0 0 x
This is equivalent to (and as fast as) an iterative version with a loop.
Haskell has tuples which are enclosed in parenthesis and separated by commas:
person = ("Bob", 42)
Tuples can be used to group multiple different values together. Haskell provides the fst and snd functions which take the respective values. These only work with pairs.
> fst person
"Bob"
> snd person
42
Haskell's pattern matching can deconstruct and match tuples.
Here we create a function called info that returns info on
a person based on the values in a tuple:
info ("", age) = "Person has no name but is " ++ (show age) ++ " years old."
info (name, 0) = name ++ " has no age!"
info (name, age) = name ++ " is " ++ (show age) ++ " years old."
This is sort of like function overloading, except the different functions are called based on the value of the parameters instead of their types.
Lists are the most common data structure in Haskell. Like Racket, these are linked lists and not arrays. They are written in brackets separated by commas:
nums = [1, 2, 3, 4]
Lists must be homogeneous and can be nested.
Haskell provides a .. operator to build a range:
nums = [1 .. 100]
Strings are simply lists of Char values:
name1 = ['B', 'o', 'b']
Equivalently:
name2 = "Bob"
Lists (and therefore also strings) can be added with ++:
nums = [1, 2, 3] ++ [4, 5, 6]
Lists can be indexed with the !! operator:
nums = [0 ..]
nums !! 100
Note that indexing a list with this operator is a linear time operation, because linked lists cannot be directly indexed.
The length of any list can be found with the length function.
To add one element to the front of a list, the : operator (which is called the "cons" operator) is used:
nums = 1 : [2, 3]
This can also be used with Haskell's pattern matching. We can write a sum function using this:
sumList [] = 0
sumList (x:xs) = x + (sum xs)
The first line is the recursive base case. It matches the empty list and returns a sum of 0 for that case.
The second line matches a non-empty list. The x portion is assigned the first item in the list. The xs portion is assigned the rest of the list. The function resolves to simply x plus the sum of the rest of the list (which is done recursively).
How can we write a function called member that takes a list of
integers and a second integer called target. It should return True if target
exists in the list, and False if not?
A higher-order function is one that takes a function as a parameter. This is extremely common in Haskell.
A common operation is to do something with a list keeping track of some accumulation. This is done in the sumList and factorial functions. We can extract this out into a function traditionally called fold:
fold f accum [] = accum
fold f accum (x:xs) = fold f (f x accum) xs
We take a function, an accumulator and a list. Folding applies the function on each element and the accumulation across the list.
This can be used to implement many things:
let sum = fold (+) 0 [1 .. 100]
let factorial x = fold (*) 1 [1 .. x]
let max nums = fold (\ a b -> if a > b then a else b) 0 nums
The fold function is actually included in Haskell in two forms foldl and foldr which are more or less the same, but reverse the arguments to the function f.
Another common higher order function is map. Map takes a function that transforms one piece of data into another, and a list. It then returns another list where the function has been applied to each item.
map (\ x -> x ^ 2) [1 .. 10]
map Char.toUpper "hello!"
How can we use map to generate a list of the lengths of a list of strings?
-- make a list of the lengths of ["bob", "alice", "george", "mark"]
map length ["bob", "alice", "george", "mark"]
How can we implement map?
Another common list function is filter. Here we are take a function that takes one parameter and returns a Bool. It also takes a list and filters out only those elements for which the function returns true:
evens = filter (\ x -> if (x `mod` 2) == 0 then True else False) [1 .. 100]
How can we write a function that takes a list of strings, and returns the ones with non-zero length?
-- filter out empty strings
filter (\ x -> if (length x) == 0 then False else True) ["a", "", "b", "", "c"]
Filter can also be used to implement the quicksort algorithm very succinctly:
qsort [] = []
qsort (x:xs) = (qsort (filter (< x) xs)) ++ [x] ++ (qsort (filter (>= x) xs))
How can the filter function be written?
As another example, recall that in math, a derivative is defined as:
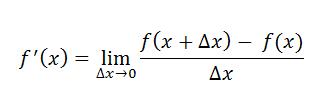
We can write a higher-order function to apply differentiation to a function:
-- take a function f and return the derivative f'
derivative f =
\ x -> (f (x + 0.00001) - (f x)) / 0.00001
This function takes a function f as a parameter, then returns another function using the definition of a derivative.
Haskell does not have variables, but we can create named values inside of functions with "let". The form of a let binding is:
let <name> = <value> in
double x =
let add a b = a + b in
add x x
We can use this to make the derivative function a bit more readable:
derivative f =
let dx = 0.00001 in
let f' x = (f (x + dx) - (f x)) / dx in
f'
Haskell supports list comprehensions which is a nice notation to create lists. The form is:
[<value> | <clause1>, <clause2>]
The value describes one element in the list. The clauses give rules describing the values.
let evens = [x | x <- [1 .. 100], x `mod` 2 == 0]
let pairs = [(a, b) | a <- [1 .. 5], b <- [1 .. 5]]
How could we make the pairs combinations of a and b instead of permutations?
-- pairs without order
let pairs = [(a, b) | a <- [1 .. 5], b <- [1 .. 5], a <= b]
Haskell has discriminated unions which are somewhat like enums. They are defined as data types before they can be used The syntax for this is:
data Name = Constructor1 Type1 | Constructor2 Type2 ...
For example, we can make a type that can store an Int or String as:
data Id = Number Int | Name [Char]
Then we can create values of type Id using the constructor:
let id1 = Number 100
let id2 = Name "Bob"
The type portion is optional. This allows us to use enums more like in C:
data Direction = North | South | East | West
dir = South
We can also use type parameters in the union. Type parameters are lower-case and typically single letters.
This allows the type to be generic across many types (like templates or generics). For example, defining a binary tree in Haskell is quite simple:
data Tree a = Leaf | Node (Tree a) a (Tree a)
This creates a tree data type which can either be a leaf, or a node which contains a left child, a value, and a right child.
We can then build tree values:
-- a tree with just one data item
let tree1 = Node (Leaf) 5 (Leaf)
-- a tree with three data items
let tree2 = Node (Node (Leaf) "A" (Leaf)) "B" (Node (Leaf) "C" (Leaf))
We can use Haskell's pattern matching with unions as well. For example, we can write a function that inserts an item into a tree:
-- base case, add to empty tree
insert Leaf item = Node (Leaf) item (Leaf)
-- add to an inner node
insert (Node left this right) item =
if item < this then Node (insert left item) this right
else Node left this (insert right item)
To see our values, we can write a traversal function:
-- traverse the list (return a string)
traverse Leaf = ""
traverse (Node left this right) =
(traverse left) ++ (show this) ++ " " ++ (traverse right)
Now we can use these functions to sort a list into a tree:
let tree = foldl insert (Leaf) [5, 6, 1, 99, 23, 42, 2, 18, 78]
traverse tree
Haskell requires every option to be handled in a function!
We have seen many data types in Haskell, now we will talk about how they're represented. In ghci, there is a special function :t that displays the type of any value.
> let x = 5
> :t x
> :t tree
> :t "Name"
> :t ("Name", True)
The :: operator is read "has type".
Haskell has type classes which are categories of related types:
> :t 5
> let x = 5
> :t x
> :t 5.5
> let y = 5.5
> :t y
"Num" and "Fractional" are generic type classes while Integer and Double are specific ones. This allows for code to be written for a type class and work for several types.
Haskell is strongly, statically typed. If there is an error, Haskell will report an error:
> "Hey" + "There"
:7:7:
No instance for (Num [Char])
arising from a use of `+'
Possible fix: add an instance declaration for (Num [Char])
In the expression: "Hey" + "There"
In an equation for `it': it = "Hey" + "There"
Haskell allows type annotations:
let x = 5 :: DoubleWhat if we ask ghci for the type of a function?
> let add x y = x + y
> :t add
add :: Num a => a -> a -> a
The "Num a =>" portion says that a is a member of the Num class. The next "a -> a -> a" portion says that the function takes two a parameters and returns an a value.
How about the types of built-in functions:
If you mistake the order of parameters, it will produce a type error:
> foldl 0 (+) [1 .. 100]
No instance for (Num ((a0 -> a0 -> a0) -> b0 -> a0 -> a0 -> a0))
arising from the literal `0'
Possible fix:
add an instance declaration for
(Num ((a0 -> a0 -> a0) -> b0 -> a0 -> a0 -> a0))
In the first argument of `foldl', namely `0'
In the expression: foldl 0 (+) [1 .. 100]
In an equation for `it': it = foldl 0 (+) [1 .. 100]
The reason Haskell uses the -> notation for functions is because functions really never take more than one parameter. The function add has the type:
add :: Num a => a -> a -> a
add 3 4
(add 3) 4
We can also only supply the first parameter of the function. What we get back is a function that takes the second parameter only:
> let add7 = add 7
> add7 5
This is called partial function application or currying.
This can be used to create new functions by customizing existing functions. For example we can define a sum function in terms of foldl:
> let sum = foldl (+) 0
> :t sum
> sum [1 .. 100]
Here we have left off the last parameter, the list, so a function is returned as sum. The function sum takes a list and returns what foldl would return, the final number.
We can also curry map to get a function that capitalizes an entire string:
> let capitalize = map Char.toUpper
> :t capitalize
> capitalize "Hello"
We can only partially supply the first set of parameters to a function. For this reason, functions like filter and map carefully choose the order of parameters to allow the most currying use.
Haskell is a pure language which means that the result of functions can only depend on the functions arguments and not cause side effects. However, this makes things like I/O hard to do. Functions like scanf depend on more than their parameters, and functions like printf cause a side effect.
By default, Haskell functions are pure. So the compiler will not allow us to do I/O in regular functions:
f x =
putStr "Checking!"
x + 1
putStr is not a function, it is an I/O action. If we want to be able to print in f, we must make it an action as well by beginning it with do:
f x = do
putStr "Checking!"
x + 1
This has changed the type of the function f:
> :t f
f :: Num (IO b) => IO b -> IO b
Because the types are all marked as being IO, we can't call this from a pure function. In this way, Haskell segregates code into pure and unpure partitions.
Using I/O in Haskell can be tricky to get right. This program reads in a user name and greets them:
-- IO action to greet
greet name = do
putStrLn ("Hello " ++ name ++ "!")
-- when compiling, main is always an IO action
main = do
putStrLn "Enter your name: "
name <- getLine
greet name
Doing I/O in Haskell is using a totally separate portion of the language. IO actions can call pure functions, but not the other way around.
As a final Haskell example, here is a Tic-tac-toe program. There are pure functions for placing moves, determining the winner, and the perfect AI, and IO actions.
Copyright © 2024 Ian Finlayson | Licensed under a Creative Commons BY-NC-SA 4.0 License.