Syntax Analysis
Overview
Syntax analysis, or parsing, is the problem of translating code in language into a parse tree using a given grammar. For example, given the following program from our example grammar:
b = c + 1;
a = a - d
We want to produce the following tree:
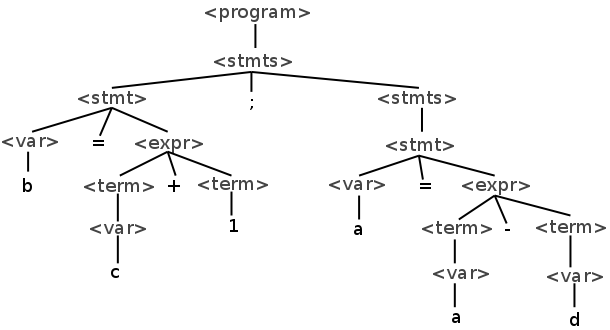
Syntax analysis comes after lexical analysis. The input to the parser is a stream of tokens and the output is a parse tree.
The parser also catches syntax errors which occur when the input program does not conform to the rules of the grammar.
Parsing
Parsing algorithms can be broadly broken into two categories:
Top-Down
Starts with the grammar's start symbol and follows the grammar rules as tokens come in. Similar to doing a derivation by hand. We will expand the left-most non-terminal, choosing which rule to apply for it based on the next token received from the lexer.
Bottom-Up
Starts with the leaf nodes of a parse tree, and replaces them with non-terminals as we go, eventually reaching the start symbol of our grammar. As tokens are received, we choose which rules to apply in the reverse order, substituting strings of symbols for non-terminals.
Parsing algorithms exist that can parse any grammar, but they are slow O(n^3). Compilers typically use algorithms that only work for a subset of grammars, but are linear. Different parsing strategies have different trade-offs in terms of performance and the limitations they place on what we can do with our grammars.
Top-Down "Recursive Descent" Parsing
In recursive descent parsing there is a function for each nonterminal in the grammar. That function is responsible for parsing strings that are matched to that nonterminal.
For the following grammar:
<expr> → <term> + <term>
| <term> - <term>
<term> → <factor> * <factor>
| <factor> / <factor>
<factor> → ID | NUMBER | ( <expr> )
We can write a recursive descent parser using the following outline:
void expr() {
/* parse the first term */
term();
/* get the + or - */
if((token != PLUS) && (token != MINUS)) {
/* parse error! */
}
/* move on to the next token */
token = lexer.nextToken();
/* parse the second term */
term();
}This function matches the expr nonterminal. The convention is that each function leaves the next token in the "token" variable.
With recursive descent, the functions that we enter and exit essentially form an in-order walk of the parse tree. A real parser would take some other action during this walk — either building a tree structure in memory, interpreting the code directly or generating intermediate code. Those actions are omitted here.
The term function would be similar:
void term() {
/* parse the first factor */
factor();
/* get the * or / */
if((token != TIMES) && (token != DIVIDE)) {
/* parse error! */
}
/* move on to the next token */
token = lexer.nextToken();
/* parse the second factor */
factor();
}Lastly, the factor could be parsed with this function:
void factor() {
/* check for the possibilities */
if(token == ID) {
token = lexer.nextToken();
} else if(token == CONST) {
token = lexer.nextToken();
} else if(token == LEFT_PARENS) {
token = lexer.nextToken();
/* parse the expression */
expr();
/* check for the closing parens */
if(token == RIGHT_PARENS) {
token = lexer.nextToken();
} else {
/* parse error! */
}
}
}LL Grammars
A recursive descent parser cannot be written for any grammar. One can be written for a class of grammar called LL. The first L refers to the fact that the parser reads the input from the left. The second refers to the fact that the parser does a leftmost derivation. LL grammars can be further categorized by the number of tokens they look ahead in the token stream. An LL(1) grammar looks one token ahead at most when deciding which action to take.
There are a few grammar constructs that an LL parser cannot handle. The first is if it must look arbitrarily many tokens ahead to determine which rule to take. If we have a grammar like this:
<ifstmt> → IF ( <expr> ) <stmt>
| IF ( <expr> ) <stmt> ELSE <stmt>
The parser cannot know ahead of time which of the two rules it will follow, because it has not yet read in all of the tokens comprising the expression and statement that are part of the if. This can be solved by left factoring the grammar which transforms the rules into this:
<ifstmt> → IF ( <expr> ) <stmt> <elseoption>
<elseoption> → ELSE <stmt> | ε
This delays the decision until the parser has read the first portion of the if.
Another issue with LL grammars is that they do not support left-recursive rules like the following:
<stmts> → <stmts> ; <stmt> | ε
If a recursive descent parser tried to parse a rule like this, it would infinitely recurse. This must be translated into an equivalent right-recursive rule like so:
<stmts> → <stmt> ; <stmts> | ε
Removing left recursion can be tricky. The following grammar is left-recursive so as
to enforce the associativity of the + and * operators:
<expr> → <expr> + <term> | <term>
<term> → <term> * NUMBER | NUMBER
Removing this left-recursion is trickier, but can be done like this:
<expr> → <term> <expr'>
<expr'> → + <term> <expr'>
| ε
<term> → NUMBER <term'>
<term'> → * NUMBER <term'>
| ε
To write a recursive-descent parser, one must re-write their grammar into an LL grammar first.
Bottom Up Parsing
In bottom up parsing, we start with the terminals and work our way up the tree. A bottom-up parser has two basic operations:
Shift
Shifting reads another input symbol from the lexer. The symbol read in is a tree with one node.
Reduce
Reducing joins existing trees as siblings of a larger tree.
During parsing, a bottom up parser maintains a parse stack holding terminals and nonterminals that have been parsed. At each step, the parser decides to either shift one token of input onto the stack, or to reduce tokens on the stack into a nonterminal using a grammar rule.
Consider the following grammar:
<stmt> → ID = <term>
<term> → <term> + <factor>
| <factor>
<factor> → <factor> * <val>
| <val>
<val> → ID | NUMBER
If we want to use this a bottom up parser to parse the code:
a = b + c * 4
Then the bottom up parser will perform the following actions:
| Step | Stack | Next Token | Input | Action |
|---|---|---|---|---|
| 0 | ID | = b + c * 4 | shift | |
| 1 | ID | = | b + c * 4 | shift |
| 2 | ID = | ID | + c * 4 | shift |
| 3 | ID = ID | + | c * 4 | reduce "val → ID" |
| 4 | ID = val | + | c * 4 | reduce "factor → val" |
| 5 | ID = factor | + | c * 4 | reduce "term → factor" |
| 6 | ID = term | + | c * 4 | shift |
| 7 | ID = term + | ID | * 4 | shift |
| 8 | ID = term + ID | * | 4 | reduce "val → ID" |
| 9 | ID = term + val | * | 4 | reduce "factor → val" |
| 10 | ID = term + factor | * | 4 | shift |
| 11 | ID = term + factor * | NUMBER | shift | |
| 12 | ID = term + factor * NUMBER | reduce "val → NUMBER" | ||
| 13 | ID = term + factor * val | reduce "factor → factor * val" | ||
| 14 | ID = term + factor | reduce "term → term + factor" | ||
| 15 | ID = term | reduce "stmt → ID = term" | ||
| 16 | stmt | Done! |
LR Grammars
The class of grammars parsable with a bottom up parser is called LR. The parser reads input from the left and produces a rightmost derivation.
For some grammars, there are times when the parser has two possible actions it can take. These are called conflicts.
A shift-reduce conflict is one where the parser could do a shift or reduce operation. Consider the following grammar:
<ifstmt> → IF ( <expr> ) <stmt>
| IF ( <expr> ) <stmt> ELSE <stmt>
If the parser is in the following state:
| Stack | Next Token | Input | Action |
|---|---|---|---|
| IF ( expr ) stmt | ELSE | ... | ??? |
Then the parser could shift or reduce. Clearly the parser in this situation should shift the else. This is called the dangling else problem and most parsers default to shifting in the presence of a shift-reduce conflict.
Reduce-reduce conflicts arise when the parser can reduce symbols on its stack to more than one nonterminal. The following grammar results in a reduce-reduce conflict:
<term> → ID * ID
<factor> → ID * ID
If the parser is in this state, it will could invoke either rule:
| Stack | Next Token | Input | Action |
|---|---|---|---|
| ID * ID | ... | ... | ??? |
While not a problem for top-down parsers, grammar rules like this are not parsable by a bottom-up parser.
Bottom up parsers are generally not written by hand, but instead generated by parser generators. They essentially convert the CFG given to them into a push-down automata which contains states for keeping track of which action should be taken and a stack.
Both strategies for parsing are widely used. We will use ANTLR for parsing which works in a top-down manner, but applies left-factoring and direct left-recursion removal to our grammars automatically.