Context-Free Grammars

Overview

After breaking the source code of a language into lexemes using lexical analysis, the next step is to discover the structure of the code: how do the lexemes group together into larger structures such as statements, expressions, loops, functions, and whatever else exits in our language.

Just as the lexical structure of a language can be specified with regular expressions, the syntactical structure can be specified with a context-free grammar (CFG). A CFG is able to express more complicated patterns than a regular expression can.

CFGs for languages are typically represented in Backus-Naur Form (BNF) which has a few elements:

Nonterminals
Symbols that represent the syntactic structures in a language such as expressions and statements. They are typically contained in < and > symbols.
Terminals
Lexemes in the language such as numbers, identifiers, key words and other symbols.
Rules
Rules have a left hand side which is a singe nonterminal and a right hand side which is a group of terminal and/or nonterminals.
A start symbol
The symbol that defines where we begin in forming the overall program from the grammar. Unless otherwise stated, this is usually the first nonterminal.

Example Grammar

Below is a very simple grammar for a small language.


<program> → <stmts>
<stmts> → <stmt> | <stmt> ; <stmts>
<stmt> → <var> = <expr>
<var> → a | b | c | d
<expr> → <term> + <term> | <term> - <term>
<term> → <var> | number

Convention has it that the first nonterminal, program, is the start symbol.

The | symbol means "or" and means that the nonterminal expands to one of the options on the right.

Notice that the <stmts> rule is recursive. That is, the nonterminal for the rule also appears on the right had side of the rule. This is really common in CFGs.

Derivations

In a derivation, we start with the start symbol and repeatedly apply the rules of the grammar. Each time, we replace one nonterminal with the symbols on the right side of a rule with that nonterminal on the left hand side.

Below is an example derivation using the grammar above:


<program>
<stmts>
<stmt> ; <stmts>
<var> = <expr> ; <stmts>
b = <expr> ; <stmts>
b = <term> + <term> ; <stmts>
b = <var> + <term> ; <stmts>
b = c + <term> ; <stmts>
b = c + 1; <stmts>
b = c + 1; <stmt>
b = c + 1; <var> = <expr>
b = c + 1; a = <expr>
b = c + 1; a = <term> - <term>
b = c + 1; a = <var> - <term>
b = c + 1; a = a - <term>
b = c + 1; a = a - <var>
b = c + 1; a = a - d

Once there are no more nonterminals, the derivation is done. The result of derivation is a sentence in the language, or a set of lexemes that follows the syntax set forth in the grammar.

There are multiple ways to perform a derivation. The derivation above is a leftmost derivation because the leftmost symbol is the one that is replaced at each step.

We can also produce a rightmost derivation where we replace the rightmost symbol at each stage, or a derivation that switches between the two.

Parse Trees

A parse tree is a visual representation of a derivation. Below is a parse tree of the example derivation above:

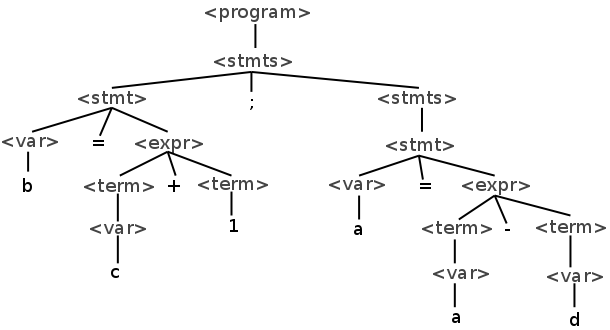
The full sentence of nonterminals can be found by doing an in-order traversal of the parse tree.

Ambiguity

A grammar is ambiguous if a sentence in the grammar can have multiple distinct parse trees. Consider the following grammar for mathematical expressions:


<expr> → <expr> <op> <expr> | number
<op> → + | *

This grammar can be used to generate expressions like the following:


1 + 2 * 3

However this expression has two distinct parse trees:

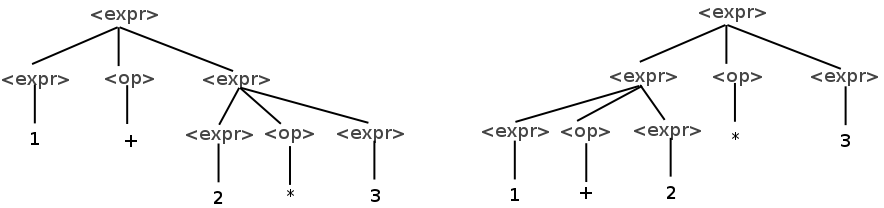
The fact that the precedence of operators is not enforced by the grammar gives this code two possible interpretations. On the left, multiplication is given the higher precedence, and on the right, addition is.

In order to avoid this, we can design the grammar to enforce the rule that the multiplication has higher precedence. The following grammar does this:


<expr> → <expr> + <term> | <term>
<term> → <term> * number | number

Here, the only possible parse tree has the multiplication done first.

Syntax vs. Semantics

Syntax refers to the grammatical structure of programs while semantics refers to what those structures mean. A CFG captures syntax but not semantics. For example, the rule in C-based languages that a variable must be declared before it is used. The correct use of a variable depends on the context in which it is used.

The following C program is syntactically correctly, but has semantic errors in it:


int main() {
    x = 5;
    int x;
    if (3 < *x) {
        float b = "hey";
    }
    return 3.5 - "";
}

We can either check for things like this while doing syntax analysis, or after syntax analysis is completed.

Non Context-Free Languages

The C++ programming language is actually not context-free. Consider the following code:


a b(c);

Looking at this code, there are two possible interpretations based on what "c" means.

If c is a type, then this is a function declaration of a function named "b" which returns a value of type "a" and takes one parameter of type "c".

If c is a variable, then this declares a variable of type "a" named "b" and passes the variable "c" to the constructor of "a" for initialization.

This means it's impossible to write a context-free grammar to fully recognize the C++ language, we need the context of what kind of identifier "c" is. C++ parsers must have extra logic for deciding how to parse code like this. Most other common languages can are context-free.