Huffman Coding Continued

Finding the Code Words

Now that we have the Huffman tree, the code for each symbol is given by the position in the tree from the root:

Following the left branch is a "0".
Following the right branch is a "1".

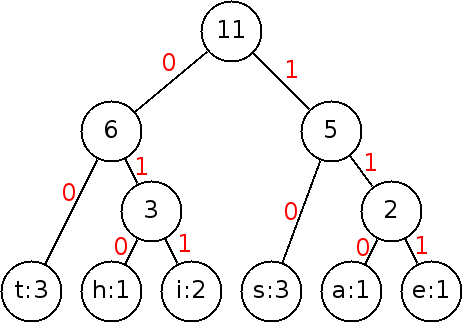
The tree from above is annotated with numbers showing the codes for each
symbol. Each left edge is labelled '0' and each right edge is labelled '1'. — The codes are given by the tree structure

This gives us the code:

Symbol	Code
t	00
h	010
i	011
s	10
a	110
e	111

Observations:

This is a prefix code, meaning we don't need to separate words even though it's variable length.
The two-bit symbols are 't' and 's' the most common, saving space.

In order to find the code for a letter, we need to traverse the tree looking for the letter, keeping track of which path we take.

For efficiency, it's best to find the codes for each letter first, and save them. This can be done recursively:

Starting at a given node, with a partial code P:
1. If this is a letter, save P as the code for this letter and return.
2. Recurse to the left with P + "0".
3. Recurse to the right with P + "1".

Compressing Text

To compress text, we simply have to substitute the letter we want with the code it maps to:


t    h     i     s    i     s    a     t    e     s    t
00   010   011   10   011   10   110   00   111   10   00

This seems like it takes more room until you remember characters are usually stored in 8-bit ASCII. With this Huffman code, we can store each letter with 2 or 3 bits.

Ignoring spaces, we cut the text from 88 bits down to 27 bits.

Example

Huffman.java implements Huffman coding for all lowercase letters. The relative probability of the letters are used to compress English text. This file uses a min heap based on our priority queue class from last class. That file is available as MinHeap.java.

The program uses the algorithms presented above to produce the tree, and find the code for each letter.

It then reads in a file of lower-case letters and writes an output file giving the compressed version.

Conclusion

A more complete text compression program would also handle:

Upper-case letters.
Spaces.
Symbols & numbers.
Decompression.

Often, Huffman trees are geared towards a particular type of data where we use all we know about the data to build the tree. This algorithm is often used as the basis for more complex compressions such as jpeg and mp3.