Dijkstra's Algorithm

Shortest Paths

One common problem is that of finding the shortest path between two nodes in a graph. This has applications in transportation and navigation such as GPS systems or Google Maps. It is also a problem faced by routers in a computer network when they decide how to route data across a network.

Below is an undirected, weighted graph representing several cities in Virginia along with approximate distances between them. Given a graph like this, we would like to find the shortest path between any two cities.

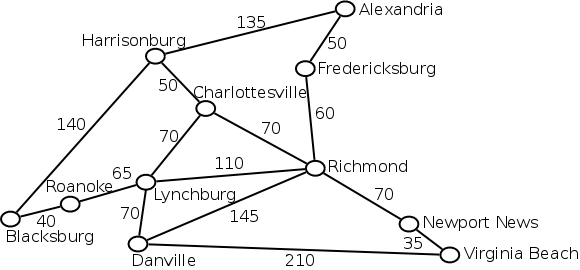
A graph of 11 cities in Virginia, connected by edges. The
edges have rough weights with the rough distances between them. — Cities in Virginia

The Algorithm

The most common algorithm to solve this problem is called "Dijkstra's algorithm". The algorithm works by finding the distance from the start node to every other node in the graph. The algorithm starts by assuming that all of the distances are infinity. It then searches out and replaces these distances with better ones as it finds them.

The algorithm stores the nodes in a min-heap, so as to process the nodes that have the least tentative distance first. As it sees each node, it looks at all of its neighbors. For each neighbor, it checks if the path through this current node is better than what it's seen so far. If so, it updates the node with this new, shorter path.

When every node has been thus processed, it prints the cost to the final node. The algorithm is given below:

Set the tentative distance to every node to infinity.
Set the tentative distance to the start node to 0.
Create a min-heap of nodes to store both the node index and tentative distance.
Insert into the heap the starting node.
While the heap is not empty:
1. Set current to heap.dequeue()
2. For each neighbor of the current node:
  1. Find the distance to this neighbor through the current node. This is the tentative distance to current + the edge weight from current to neighbor.
  2. If this distance is less than the tentative distance to the neighbor we have so far, then replace it and insert a node into the heap for neighbor with the new cost.
Return the tentative distance to the end node which is now minimal.

Dijkstra's algorithm is implemented in this example. Notice that we insert each edge in both directions because we assume each street is a two-way street.

Analysis

Analyzing graph algorithms can be a bit tricky because we don't just have one $N$. We have the number of nodes in the graph, which is often denoted as $V$ (for vertices). We also have the number of edges which is $E$.

The analysis of this algorithm depends on whether we are using an adjacency matrix or incidence list, how dense the graph is, and how we implement the algorithm.

Looking at the algorithm above, step 1 takes $O(V)$ time, because we need to set the tentative cost for each node. Steps 2 through 4 take a constant amount of time, $O(1)$.

The loop that runs through the nodes in the min-heap will iterate at most $O(V)$ times, because the nodes are added to the heap as discovered. Inside the loop we dequeue a node from our heap which takes $O(\log V)$ time.

We also need to loop through each of the neighbors, which is $O(V)$ iterations. For each one, we might need to insert it into the min-heap which would give us $O(\log V)$. So the whole loop is $O(V \log V)$. Based on all of this, the running time is:

$V + V \times (\log V + V\log V)$

We can simplify this as:

$V + V\log V + V^2\log V$

$O(V^2\log V)$