Heap Operations

Insertion

To insert an item into the heap, we will need to maintain the heap property. To do this we will start by inserting the item into the next available array location, and then fix the heap. Fixing the heap after an insertion is called upheaping.

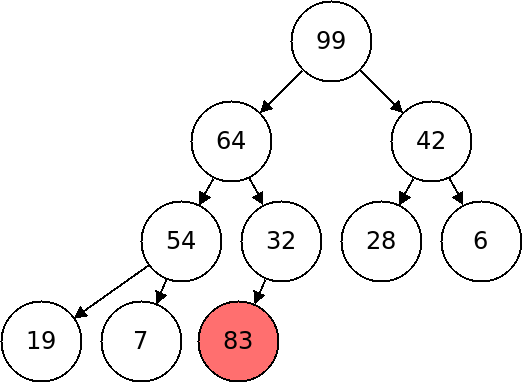
The value 83 was inserted into a heap in the next available slot in the bottom.
It is below 32 which is not right. — Step 1: Insert in the next available slot

The above heap has an element (in red) inserted in the next available location. To fix the heap, we will test if the item we inserted is less than its parent. If not we will swap the node with its parent.

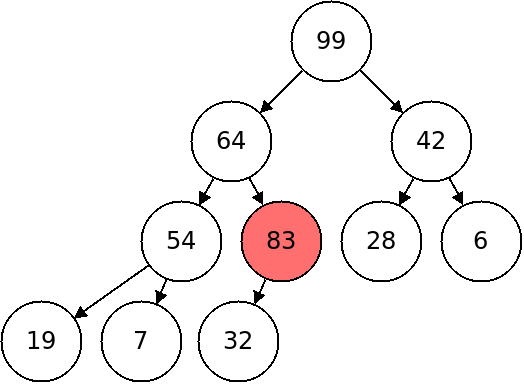
The value 83 has been swapped with its parent of 32. Now its parent is
64 which is still not right. — Step 2: Upheap by swapping places with parent

In the above heap, we swapped 83 with its parent 32. We will repeat this process until the parent is greater, or the node we inserted becomes the root.

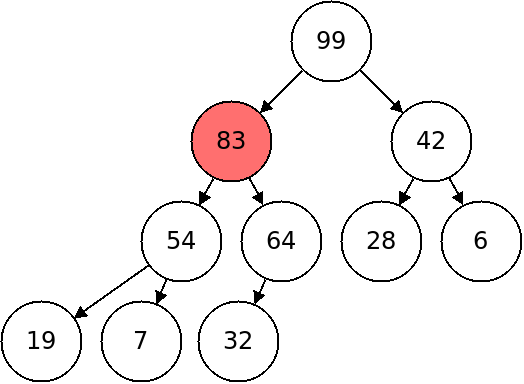
The value 83 has been swapped with its parent of 64. Now its parent is
99 which is right. — Step 3: Upheap again, now we are good

This heap shows the final result of inserting 83.

The algorithm for insertion is given below:

Insert the item at the next available location.
While the item is not the root, and it has a greater value than its parent:
1. Swap the item with its parent.

Below is a method for insertion for a class which stores integers in a heap:


// insert an item into the heap
public void insert(int item) {
    // put the new one in the next slot
    array[count] = item;
    int node = count;
    int p = parent(node);
    count++;

    // upheap it until it is under a node which is bigger than it (or the root)
    while ((node != 0) && (array[node] > array[p])) {
        int temp = array[node];
        array[node] = array[p];
        array[p] = temp;

        node = p;
        p = parent(node);
    }
}

What is the Big-O of the insertion algorithm?

Well, actually putting the data into the next available slot takes a constant amount of time. The only part that loops is the upheaping loop. So how many times could we have to upheap? The worst case scenario is that we need to upheap all the way to the top. Luckily we know that the tree is perfectly balanced. In a balanced tree with $N$ nodes, there are no more than $log_2(N)$ levels. So the insertion is $O(\log N)$.

Removing the Top

When we want to find the max element, it will be stored in the top of the heap. Typically, when we look at the top of the heap, we will also want to remove that item. In the heap below, for example, we would want to remove the root element, 99.

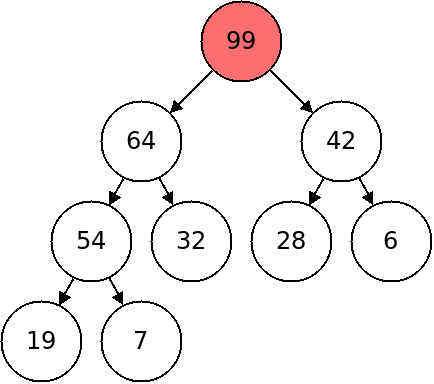
The heap shows the root node, storing 99, highlighted because we want
to remove it — We want to remove the root

After deletion, we need to maintain the property that the heap is fully left aligned. This means that the spot we need to remove is the rightmost one in the bottom level.

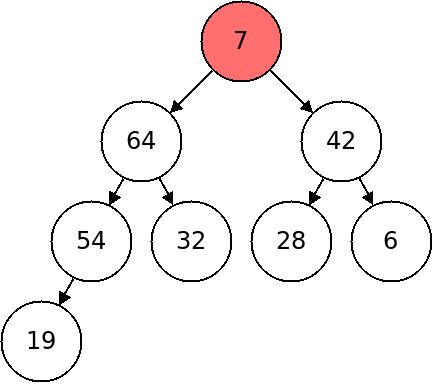
We have taken a value of 7, which was on the bottom of the heap, and
wrote it over the top of the 99 in the root node. The node containing
7 is now gone. — Step 1: Swap with the right-most one on bottom

So to delete the root, we will swap it with the last element in the bottom level (as illustrated above). Then we will remove the last element in the bottom. Finally we will fix the heap by downheaping.

To downheap, we will check if the item is bigger than both children, if not we will swap it with its larger child and repeat. This is illustrated below:

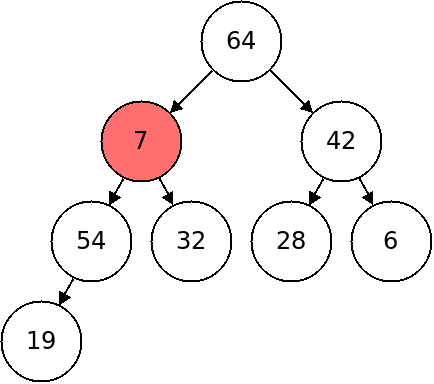
The 7 has been swapped with the larger of its children, a 64. — Step 2: Downheap to swap 7 and 64

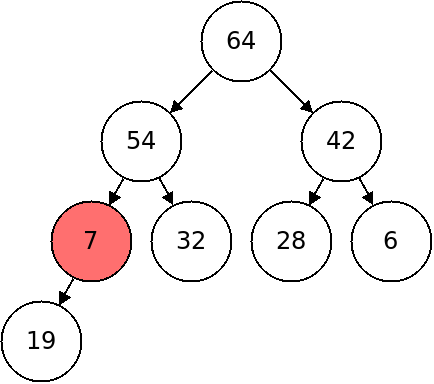
The 7 has now been swapped with the larger of its children again, a 54 — Step 3: Downheap again to swap 7 and 54

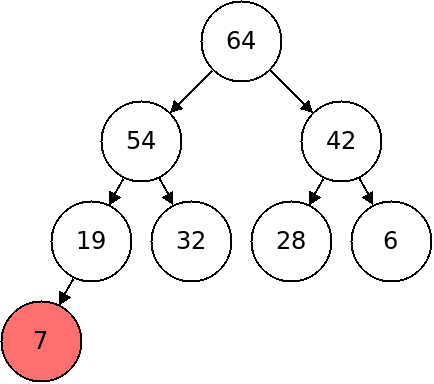
The 7 has again been swapped with the larger of its children, a 19 — Step 4: Downheap one last time to swap the 7 and 19

In pseudocode:

Save the root as the return value.
Move the last child to the root.
While one of the children of this node has a greater value:
1. Find the largest of the children.
2. Swap the largest child with this node.
Return the original value.

In Java:


    // remove the top item
    public int dequeue() {
        // save the item to return it
        int value = array[0];

        // move the last item to the root and decrement
        array[0] = array[count - 1];
        count--;

        // find the children
        int node = 0;
        int l = left(node);
        int r = right(node);

        // while one of the children is bigger - or equal
        while (((l < count) && (array[l] > array[node])) ||
                ((r < count) && (array[r] > array[node]))) {

            // find the larger node
            int max;

            // if there are two, take larger
            if ((l < count) && (r < count)) {
                if (array[l] > array[r])
                    max = l;
                else
                    max = r;
            }
            // if just one take that one
            else if (l < count) {
                max = l;
            } else {
                max = r;
            }

            // swap them
            int temp = array[max];
            array[max] = array[node];
            array[node] = temp;

            node = max;
            l = left(node);
            r = right(node);
        }

        return value;
    }

Like insertion, this algorithm only has one loop in it, which loops for as many times as we need to downheap. For the same reasons, that makes it $O(\log N)$.

A full example of a heap storing integers can be seen in HeapExample.java.