Binary Search Trees Removal

 

Removing Nodes

Removing a node from a binary search tree is a bit more complicated than inserting or searching one.

If we want to remove a particular element from a tree, we must first search for the node with that value (using the searching algorithm described above). However, once we find the data we want to remove, there are three different cases.

  1. The node is a leaf:

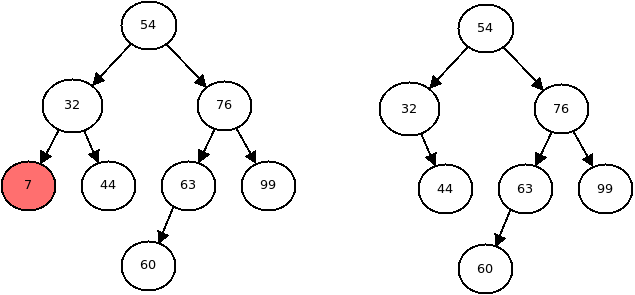
    There are two binary search trees. The first shows a leaf node we would like to remove. The second shows that node simply gone. Its parent now just points to nothing on that side
    Removing a leaf node

    In this case, we can simply remove the node, and set the link to it to null.

  2. The node has one child:

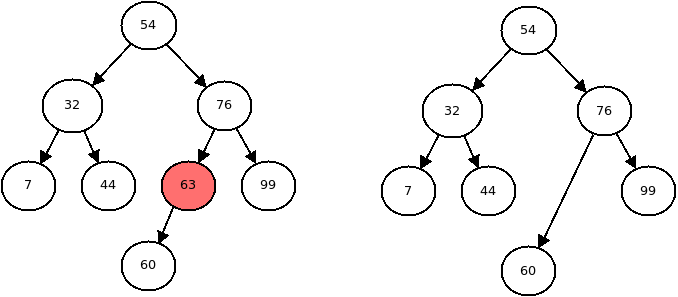
    There are two binary search trees. The first shows a node we would like to remove that has one child. The second shows that node gone. Its parent now links to its one child instead of it.
    Removing a node with one child

    In this case, we must set the parents pointer equal to the node's only child.

  3. The node has two children:

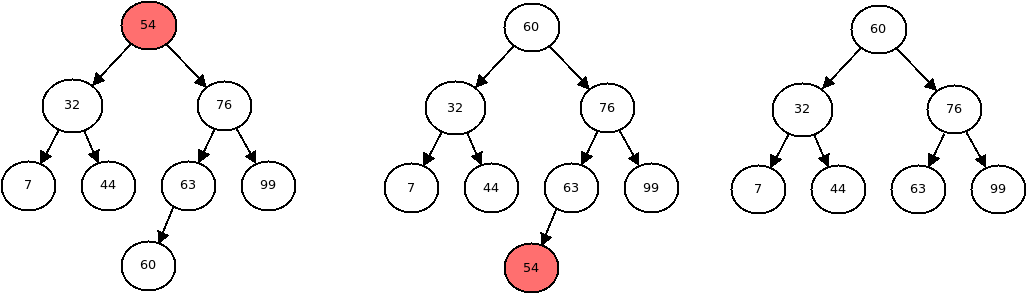
    There are three binary search trees. The first shows a node we would like to remove with two children. In the second, we have swapped the data between the node we're removing and the smallest value node on the right subtree. In the third we have removed that node from the right subtree which used to have the smallest value.
    Removing a node with two children

    This is the most complicated case.

    If we just remove the node, then the tree will be split into two pieces so it will no longer be a tree. We will need to find a new root of the subtree that we are deleting. We also must obey the rules governing binary search trees, so we can't use any node for the new node.

    There are only two nodes that we can use for the new root, either the smallest value on the right, or the largest value on the left.

    We can then swap the data at those two nodes, as shown in the center picture above. Then there will be a duplicate node, so we must then delete that one (which we can do recursively).

 

Algorithm

The algorithm to remove a node from a binary search tree is as follows:

  1. If the node has no children, return null to its parent.
  2. If the node has only a left child, return node.left to its parent, bypassing it.
  3. If the node has only a right child, return node.right to its parent, bypassing it.
  4. If the node has two children:
    1. Find the node with the least value in the node.right subtree.
    2. Swap the data at the least node with the one we want to remove.
    3. Remove the least node.

To find the smallest node on a subtree we can use the following algorithm:

  1. If the node at the root of the subtree has no left child, return the data at the root.
  2. Otherwise recursively find the smallest node on the left subtree.

BinarySearchTree.java contains all of the necessary code dealing with binary search trees so far, including inserting, searching, and now removing.