Binary Search Trees

Overview

A binary tree is a specific kind of tree, and a binary search tree is a specific kind of binary tree. Specifically it is a binary tree that obeys the following rules:

The left subtree of a node N contains only nodes with values less than that of the node N.
The right subtree of a node N contains only nodes with values greater than that of the node N.
No two nodes can have the same value.

Below is an example of a binary tree that is also a binary search tree:

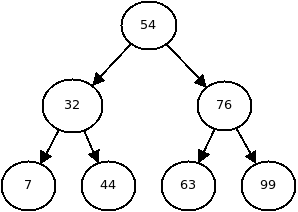
This binary tree has numbers stored in each node. For each node, all
the numbers to the left have values smaller, while all nodes to the right
have values larger. — A binary search tree

The goal of binary search trees is to store data in a way that is amenable to the binary search algorithm. To search a tree for an item, we can start at the root node and compare the value there to the target. If the target is larger, then we know that the target must be in the right subtree and if the target is smaller, we know the target is in the left subtree.

Recall that with binary search we can search a sorted array in $O(\log n)$ time. We can also search a binary search tree in $O(\log n)$ time. However the advantage of a binary search tree is that we can also insert quickly.

Inserting

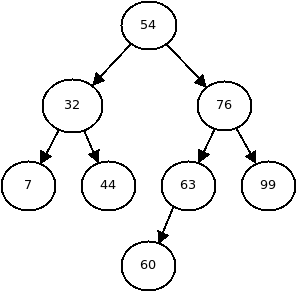
If we are to insert a new value 60 into the tree above, where should it go?

We can't violate the rule that the nodes in the left subtree must be less than that of the node. So 60 must be inserted to the right side of the root node 56. Then we look at the root of the right subtree, 76. 60 is less than 76 so it must go in the left subtree of the 76 node. Then we get to the node 63, and 60 is less than that node, so it must go in the left subtree. There is no left subtree of this node, so we create one to store our new node and are done.

This is what the tree will look like after inserting 60:

This binary search tree is the same as the previous one, except that
the value 60 has been inserted as the left child of 63. — The tree after inserting 60

Given a binary search tree and a new item to insert into it, there is always exactly one place that we can put it.

The algorithm to insert into a binary search tree looks like this:

To insert a value at a given node:
1. If the node is null, create a new node here with the value.
2. Otherwise, if the data at this node is less than the new value:
  Insert the value in the right subtree.
3. Otherwise, if the data at this node is greater than the new value:
  Insert the value in the left subtree.

Here is the code for doing the insertion in Java:


// recursive function to insert at a particular node
private Node insertAt(Type value, Node node) {
    // if this part of the tree is empty, return a new node
    if (node == null) {
        return new Node(value);
    }

    // otherwise, insert into the appropriate side recursively
    if (node.data.compareTo(value) < 0) {
        node.right = insertAt(value, node.right);
    } else {
        node.left = insertAt(value, node.left);
    }

    return node;
}

// insert a number calls recursive function to insert at the root
public void insert(Type value) {
    root = insertAt(value, root);
}

Like other recursive methods, there are actually two methods here. The first one does the bulk of the work, but needs an extra parameter, indicating where in the tree we are looking. The second just supplies the starting value of the root node.

Also notice that the method is returning the node it's creating. The reason for that is that we need to assign the node into the reference that points to it (which is either root or one of the left/right references).

Searching

Searching a binary search tree uses the same basic idea behind regular binary search and is similar to the insertion algorithm above. At each step of the search, we consider a node and there are four possibilities. Either the node is null, in which case the item doesn't exist in the tree. Or the node has the data we want in which case we have found what we were searching for. Or the node has a value that is less than the item we are searching for, in which case we must search the right subtree. Or the node has a value that is more than the item we are searching for, in which case we must search the left subtree. We will start at the root and recursively work our way down.

This can be summarized in the following algorithm:

To search for a target at a given node:
1. If the node is null, return not found.
2. If the node has the data, return it.
3. If the node's value is less than target, search the right subtree.
4. Otherwise, search left subtree.

Here is this algorithm expressed in Java code:


// recursive function to search starting at a particular node it
private Node searchAt(Type target, Node node) {
    if (node == null) {
        return null;
    } else if (node.data.equals(target)) {
        return node;
    } else if (node.data.compareTo(target) < 0) {
        return searchAt(target, node.right);
    } else {
        return searchAt(target, node.left);
    }
}

// search for a value starting at the root
public Type search(Type target) {
    Node node = searchAt(target, root);
    if (node == null) {
        return null;
    } else {
        return node.data;
    }
}

Here the non-recursive helper method also takes the Node that was returned and pulls the data out of it.