Merge Sort

The algorithm

The last sort function we will look at is a little different. It uses recursion and is also, generally, much more efficient than bubble sort.

The basic approach is to split the array into two halves, a left half and a right half. Then we sort each half. Then to finish up, we merge the two sorted halve back together. We will talk about how to merge the halves in a bit.

This algorithm is recursive because, in defining how we sort an array, we sort two smaller arrays. We need to add a base case. In the case of sorting, our base case is when the array has zero or one elements (these arrays are already sorted). The algorithm can be expressed as:

To Mergesort an array:
1. If the array has 0 or 1 items, we're done.
2. Mergesort the left half.
3. Mergesort the right half.
4. Merge the two halves together to make a new, sorted, array.

This can be converted into a recursive function:


public static void mergeSort(int[] array, int start, int end) {
    if (start < end) {
        int middle = (start + end) / 2;

        // sort left half
        mergeSort(array, start, middle);

        // sort right half
        mergeSort(array, middle + 1, end);

        // merge the two halves
        merge(array, start, end);
    }
}

public static void mergeSort(int[] array) {
    mergeSort(array, 0, array.length - 1);
}

Now all we need to do is figure out how to merge two arrays back together. The way we will do this is by looking at both arrays. We will take the first value from the array with the smallest number. Then we will do this again and again until one of the arrays runs out. Then we'll add the rest of the remaining array in.

The merge algorithm can be expressed as:

Set the result array to empty.
While both of the arrays have data:
1. If the left array value is less than that of the right array, add the left array value to result.
2. Otherwise, add the right array value.
Add the rest of the remaining array to the result array.

In Java code, that looks like this:


public static void merge(int[] array, int start, int end) {
    int middle = (start + end) / 2;
    int temp_index = 0;

    // create a temporary array
    int[] temp = new int[end - start + 1];

    // merge in sorted data from the 2 halves
    int left = start;
    int right = middle + 1;

    // while both halves have data
    while ((left <= middle) && (right <= end)) {
        // if the left half value is less than right
        if (array[left] < array[right]) {
            // take from left
            temp[temp_index] = array[left];
            temp_index++;
            left++;
        }
        else {
            // take from right
            temp[temp_index] = array[right];
            temp_index++;
            right++;
        }
    }

    // add the remaining elements from the left half
    while (left <= middle) {
        temp[temp_index] = array[left];
        temp_index++;
        left++;
    }

    // add the remaining elements from the right half
    while (right <= end) {
        temp[temp_index] = array[right];
        temp_index++;
        right++;
    }

    // move from temp array to the original array
    for (int i = start; i <= end; i++) {
        array[i] = temp[i - start];
    }
}

With the merge function, we can complete a merge sort program.

Mergesort Analysis

Merge sort is a little more complicated to analyze due to the recursion. The first thing to do is analyze the merge algorithm. This algorithm loops through the array from start to end, merging elements as we go along. It should be clear that this algorithm takes an amount of time proportional to the size of the array, so it's $O(n)$.

Next we have to look at the whole mergesort algorithm. The algorithm works by calling itself twice on half the input size, then merging the results with the merge algorithm. We can express the time $T$ taken by this algorithm with the following recurrence relation:

$T(n) = 2 \cdot T(\frac{n}{2}) + n$

This is saying that the time taken to mergesort an array of size $n$ is twice the time taken to sort an array half that size (the two recursive calls), plus the $n$ time needed to do the merge.

This is a recurrence relation which is a relation which is recursive, because in defining $T(n)$, we have a reference to the relation $T$. This doesn't in an of itself tell us anything helpful.

To try to make sense of this relation, we can go ahead and plug in the value of $T(\frac{n}{2})$ using the recurrence relation:

$T(n) = 2 \cdot (2T(\frac{n}{4}) + \frac{n}{2}) + n$

Simplifying gives us:

$T(n) = 4 \cdot T(\frac{n}{4}) + 2n$

Expanding again gives us:

$T(n) = 4 \cdot (2T(\frac{n}{8}) + \frac{n}{4}) + 2n$

Simplifying gives us:

$T(n) = 8 \cdot T(\frac{n}{8}) + 3n$

Expand again:

$T(n) = 8 \cdot (2T(\frac{n}{16}) + \frac{n}{8}) + 3n$

Simplify again:

$T(n) = 16 \cdot T(\frac{n}{16}) + 4n$

It should be clear that there is a pattern emerging. No matter how many times we expand this out, we will get something of the form:

$T(n) = 2^k \cdot T(\frac{n}{2^k}) + kn$

Where $k$ is the number of times we expand the formula.

The question then becomes how many times do we expand the formula? How many times does the mergesort algorithm recurse?

The answer is the number of times we can divide the array in half before we hit the base case. How many times can a number $n$ be divided by 2 until we hit 1? The answer is $log_2(n)$ times.

If we substitute $k = log_2(n)$ in our formula, we get:

$T(n) = 2^{log2(n)} \cdot T(n / 2^{log2(n)}) + log2(n) \cdot n$

Then we can use the fact that an exponent and a logarithm are opposite operations to get:

$T(n) = n\cdot T(1) + log2(n) \cdot n$

The value $T(1)$ is the time taken to mergesort an array with 1 item. This is the base case and can be done in constant time (one item is always sorted). That gives us:

$T(n) = n\cdot log2(n) + n$

When we use Big-O notation, we only care about the term that dominates. The extra "+ n" is relatively unimportant for large values of n because the other part is larger. Also the base of the logarithm is not necessary to state (it is essentially a constant factor) Thus we can say:

$T(n) = O(n\cdot log(n))$

This means that the algorithm is faster than a $O(n^2)$ one (like bubble sort), but not as fast as a linear algorithm:

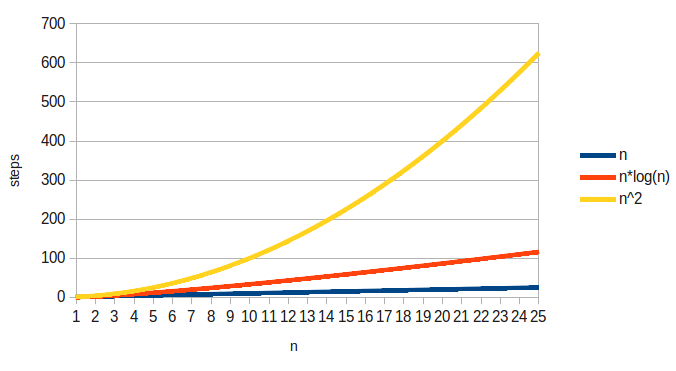
A graph showing n squared, n log n, and n. The n squared line
is the highest, then n log n, and then n is the lowest — Comparison of n log(n) to other complexities

Mergesort is significantly faster than simpler sorts like bubble sort for large input sizes. It actually turns out that $O(n \log{} n)$ is the best we can do for general purpose sorting algorithms. There are a few other sorting algorithms with this complexity including quicksort, and heapsort (which we will look at when we get to heaps).