The example last time has a serious issue, which is that it doesn't handle collisions. A collision occurs when the hash function returns the same index for two different keys. In our simple hash method, this happens when two names have the same letters, just rearranged. For instance "Elena" and "Elane" are given the same hash code.
Because the possible number of keys is typically much larger than the number of valid indices, collisions are always possible.
One way of handling collisions is to check if the place we want to store an element is occupied. If it is, we move onto the next element, repeatedly until we find an empty slot to insert our data. This is called linear probing since we go in a line looking for an empty slot.
For example, we can rewrite our insert method like this:
// insert a person
public void insert(String name, String number) {
// get the index by hashing the key
int index = hash(name);
// linear probe until we find an empty slot
while (table[index] != null) {
index = (index + 1) % maxSize;
}
// now store it
table[index] = number;
}
Likewise, we will need to handle this in the lookup method as well. However, right now we are only storing the values (phone numbers) in the table. As it is, we won't really have any way of knowing if the number in the table is right!
For example, if we are given "Elane" as the key, and get the hash index, and then find a number there, we won't know if that's Elane's number or Elena's.
For that reason, we will need to store the values and the keys in our hash table. Then we can ensure that the key's match before returning the data.
This example extends the simpler example above in a few ways:
We start by declaring the generic class, and making arrays for storing both the keys and values:
public class HashTable<Key, Value> {
private Value[] values;
private Key[] keys;
private int maxSize;
public HashTable(int size) {
maxSize = size;
// make the arrays, with the workaround for Java not allowing generic arrays
values = (Value []) new Object[maxSize];
keys = (Key[]) new Object[maxSize];
}
Here we also allow the user to pass in the size of the table.
Next, we will write code to insert a new key, value pair.
// insert a key/value pair
public void insert(Key key, Value value) {
// get the index by hashing the key
int index = Math.abs(key.hashCode()) % maxSize;
// linear probe until we find an empty name
while (values[index] != null) {
index = (index + 1) % maxSize;
}
// insert the value and key here
values[index] = value;
keys[index] = key;
}
This code does linear probing to find an empty slot, then inserts both the key and value at that index. Notice we use the key's .hashCode() method, and ensure this is valid for our array.
Finally, we will lookup a value given its key:
// lookup a value by its key
public Value lookup(Key key) {
// get the starting index from hash function
int index = Math.abs(key.hashCode()) % maxSize;
// loop while there is data here
while (keys[index] != null) {
// if the key here matches target, return corresponding value
if (keys[index].equals(key)) {
return values[index];
}
// move to next index to search (with wrap around)
index = (index + 1) % maxSize;
}
// if we fell off the end, the key is not here
return null;
}
Here we get the hashed index using the same scheme as when inserting. Then we begin looping at that index. As we go, we check if the key in this slot equals the key we are looking for. If so, we return the associated value. We also check if this slot is null. If so, we must not be storing this key, so we return null.
The code for this is available in HashTable.java.
One problem with this code is that we don't handle the case when the array is full. As we'll discuss, we wouldn't really want to use a hash table if we think this is likely.
Another approach to solving collisions, is called "chaining". What we do here is keep the hash table as an array of linked lists. Each time we want to insert an item into the hash table, we will hash the key, which will tell us which slot in the array to use. Then the item will be appended to the given linked list.
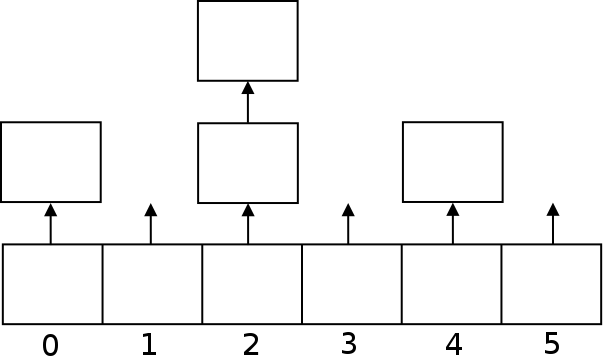
Chaining has the advantage that the hash table can never really fill up, it just gets to be less efficient as it gets bigger (because we have to search through the growing lists).
However searching through a linked list is slower than searching through an array. Also, if you think the hash table will get close to full, you should not use a hash table anyway (because you won't achieve $O(1)$ performance anyway then). So linear probing is generally more widely used.
The performance of a hash table heavily depends on the size of the table, and how good the hash function is.
In the worst case, your hash function returns the same index every time, and you have to essentially search through the whole array each time (or linked list if using chaining). That would be $O(N)$ time.
In the best case, the hash function will return a different code for each key, so all insertions and lookups are $O(1)$. It really only makes sense to use hash tables in situations when you can guarantee there will be few collisions.
You do this by making sure the hash table is bigger than the maximum amount of data being stored. It also works out better if the size of the hash table is a prime number. For example, if we wanted to store 5000 values, we could pick 71411 as the table size. This is a prime number and gives us enough empty space that there will be few runs of collisions.
Also the hash function should provide a uniform distribution of indices:
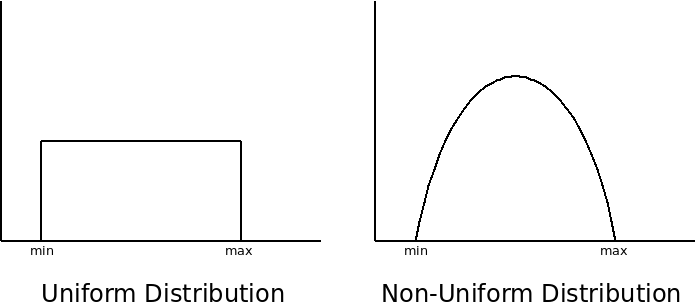
With a large table, and a well-designed hash function, there will be minimal collisions, so searching a hash table is $O(1)$ in general.
Another method for resolving collisions is called rehashing. With this technique, we would have a second hash function that is used if the first one causes a collision. If the second one also causes a collision, then we have to resort to linear probing or chaining. Rehashing avoids problems where our input function has a "spike" in one particular area of the table. Running them through a second hash function can help smooth this out.
Hash tables require more tweaking than most other data structures. The size of the table must be carefully chosen. If the table fills up too much, it slows down. Also, unlike most data structures, hash tables cannot be easily resized since the hash function would need to return new results (because we modulus by the table size).
The hash function also must be carefully chosen. If it does a poor job, performance will suffer.
If all of the data is known ahead of time, one can write a perfect hash function that assigns a different index to each piece of data. Generally though, the hash function doesn't know what data will be used ahead of time, and must try to use as uniform a distribution as possible.
If the hash table is well-tuned, it is the fastest way to store searchable data.
Copyright © 2024 Ian Finlayson | Licensed under a Creative Commons BY-NC-SA 4.0 License.