Stacks Continued

Implementing a Stack with a Linked List

One drawback of using an array to implement a stack is that we can fill up the array. We don't handle this in the example above, but if we try to push on a stack that is full, we will write past the bounds of our array. To properly handle this case, we would need to allocate a new array and copy everything over.

In order to avoid that, we can store the stack inside of a linked list instead of an array. Because we only ever care about the top of the stack, a singly-linked list will suffice. When writing a stack with a linked list, we can change the terminology a little bit and rename the next pointer to "underneath" and the head of the list to "top":


    private class Node {
        public Type data;
        Node underneath;
    }

    Node top;

In an empty stack, the top node is equal to NULL. In a stack with nodes, we always keep a pointer to the top node, which has a pointer to the one underneath it and so on. The bottom of the stack has an underneath pointer of NULL:

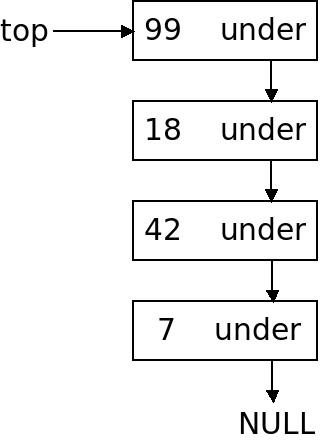
The list stack contains a top variable pointing to the top node in
the stack. Each node points to the one underneath it, with the last
pointing to null — A stack implemented as a linked list

When we push an item onto the stack, we are essentially adding at the front of the linked list. Likewise when we pop we are removing from the front of the linked list. Because stacks are more restrictive than an actual linked list, they are a bit simpler to program.

The following is an example of a simple list-based Stack class:


class Stack {
    private class Node {
        double data;
        Node underneath;
    }
    Node top;

    public Stack() {
        top = null;
    }

    public void push(double val) {
        Node newNode = new Node();
        newNode.data = val;
        newNode.underneath = top;
        top = newNode;
    }

    public double pop() {
        double value = top.data;
        top = top.underneath;
        return value;
    }

    public boolean empty() {
        return top == null;
    }
}

Reverse-Polish Notation

One application of stacks is in evaluating arithmetical expressions. We could write a program to evaluate usual arithmetical expressions (which would also involve a stack), but instead here we will evaluate Reverse Polish Notation (RPN) expressions.

RPN, also called postfix notation, is a system of writing mathematical expressions where the operator comes after the operands instead of in between. For example, we would normally write the seven plus two as:

7 + 2

In RPN, this would be written as:

7 2 +

We can combine multiple operations in RPN like so:

7 2 + 5 -

What this means is we apply + to 7 and 2 which gives us 9. Then we take the 9 and 5, then apply minus to those giving us 4. We can also have more than two numbers in a row:

1 2 3 4 + +

One big advantage of RPN is that we no longer need to use parenthesis to specify the order of operations. For example the infix operations:

(1 + 2) * 3

and:

1 + (2 * 3)

have different values. In RPN, the first one would be written as:

1 2 + 3 *

and the second would be:

1 2 3 * +

Another big advantage of RPN is that it can be more easily evaluated in a computer program. This is because we only need to scan left to right, instead of looking through the expression multiple times and following the order of precedence.

We can write a program to implement this task using a stack. To do this, we will scan through the RPN expression. Each time we see a number, we will push it onto the stack. When we see an operator we will pop two values off the stack, apply the operation to them, and push the result on the stack. At the end of the expression, the answer should be on top of the stack.

The following code implements this:


public class Calculator {
    public static void main(String args[]) {
        Stack stack = new Stack();

        Scanner in = new Scanner(System.in);
        String expression = in.nextLine();
        String[] parts = expression.split(" ");

        for (int i = 0; i < parts.length; i++) {
            try {
                double value = Double.parseDouble(parts[i]);
                stack.push(value);
            } catch (NumberFormatException e) {
                if (parts[i].equals("+")) {
                    double a = stack.pop();
                    double b = stack.pop();
                    stack.push(a + b); 
                } else if (parts[i].equals("*")) {
                    double a = stack.pop();
                    double b = stack.pop();
                    stack.push(a * b); 
                } else if (parts[i].equals("-")) {
                    double a = stack.pop();
                    double b = stack.pop();
                    stack.push(b - a); 
                } else if (parts[i].equals("/")) {
                    double a = stack.pop();
                    double b = stack.pop();
                    stack.push(b / a); 
                } else {
                    System.out.println("Error, unrecognized symbol: " + parts[i]);
                    return;
                }
            }
        }
        
        System.out.println(stack.pop());
    }
}