Assignment 5 - Course Scheduler

Objective

To gain experience using graphs and topological sorting.

Task

Directed Acyclic Graphs (DAGs) are an important type of graph with many applications. Recall that a directed graph is one where the edges have a direction. Recall that an acyclic graph is one with no cycles. A cycle is a sequence of edges in a graph where following it will lead you back to the original node. If a graph is directed and acyclic, it is a DAG.

One common usage of DAGs is to represent dependencies between different things. For example, courses in a school generally can have pre-requisites. In the computer science department, taking CPSC 340 depends on having taken CPSC 240. We can represent these pre-requisites with a DAG where an edge from course A to course B means that A is a pre-requisite of B. Below is a DAG representing the dependencies between several required courses for the computer science major:

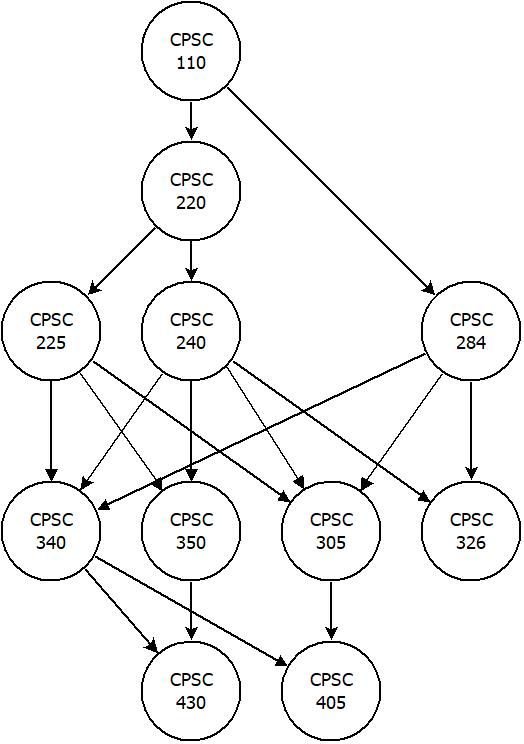
Note that if there were a cycle in this graph (such as if there were an edge going from 340 back to 110), then the graph would no longer be a DAG. It would also mean it would be impossible to complete the courses because there would be an endless loop of pre-requisites.

Given any DAG, it is possible to produce a topological ordering which is a list of the nodes in the DAG such that every node appears before the ones that it has edges pointing to. A topological ordering for the graph above is:

1. CPSC 110
2. CPSC 284
3. CPSC 220
4. CPSC 240
5. CPSC 326
6. CPSC 225
7. CPSC 350
8. CPSC 305
9. CPSC 340
10. CPSC 430
11. CPSC 405

Note that there are multiple topological orderings possible for this DAG.

The process of producing a topological ordering from a DAG is called topological sorting.

Your task for this assignment is to write a program that will take a list of courses and their pre-requisites as input, and print out a topological ordering that one can take the courses in without violating any pre-requisites. If the set of courses can not be taken in any order, you should print out that there is no way to take those courses.

Your program will be given the name of an input file on the command line. The file consists of a list of courses with their pre-requisites in the following format:

number-of-courses
course1 number-of-prereqs prereq1 prereq2 ...
course2 number-of-prereqs prereq1 prereq2 ...
...

Each course will be specified with four letters followed by 3 digits. Some courses will of course have no pre-requisites. Below are three sample input files:

• cpsc.txt: the computer science major classes as shown above
• cybr.txt: the required classes for the cybersecurity major
• impossible.txt: courses with a loop, for which there is no possible ordering

Algorithm

One algorithm for topological sorting is given below:

1. Set the ordering to empty.
2. Find the set of nodes with no edges coming into them. Call this the active set.
3. While there are nodes in the active set:
   1. Move a node N from the active set to the ordering.
   2. For each edge coming out of N and into M:
      1. Remove the edge from the graph.
      2. If M now has no edges coming into it, add it to the active set.
4. If the graph has any edges left, then there is no topological ordering!
5. Otherwise, the topological ordering is in the "ordering" list.

Details

• You can start with Graph.java which is a Graph class based on an adjacency matrix. It is set up to hold an unweighted, directed graph. You can modify this however you see fit.
• The file name for input will be given on the command line (you should also check for errors).
• You should then read the courses into a graph, setting up the nodes and edges appropriately.
• It will be easier to make two passes over the file: one to add the nodes and one to add the edges. To start back at the beginning of a file, you can just close your scanner, then open the file up again with a fresh Scanner attached to it.
• Once the graph is made, perform the topological sorting on it.
• If there is a valid topological ordering, you should print it out.
• Otherwise print out that the courses are impossible to complete.

General Requirements

• All member data of a class must be private.
• Your source code should be readable and reasonably indented.
• You must provide comments in your code.
• Your class should not cause Exceptions to be thrown in any situation.

Submitting

When you are done, submit your code for this program on Canvas.