Space Complexity

Introduction

Time complexity deals with how different problems require different amounts of time to solve. Most algorithm analysis looks at time complexity.

Space complexity deals with how different problems require different amounts of storage space to solve. As we'll see, we can also separate problems by the different amounts of space that they take to solve.

Analyzing Space

As with time complexity, we will use Turing machines as the basis for our analysis of space complexity. If $M$ is a Turing machine, we say that the space complexity of $M$ is the function $f(n)$ where $f(n)$ is the maximum number of tape cells that $M$ scans on any input of length $n$.

We talked about the $SAT$ problem which can be given as:

$SAT = \{E\; |\; E \text{ is a boolean expression that is satisfiable}\}$.

An algorithm which decides the $SAT$ problem is:

$M = $ "On input $\phi$, where $\phi$ is a Boolean formula:

For each truth assignment to the variables $x_1, x_2 ... x_m$ of $\phi$:
Evaluate $\phi$ on that truth assignment.
If it ever evaluates to true, accept. Otherwise, reject."

As we've seen, the time complexity of this algorithm is $\mathcal O(2^n)$. Because this problem is $NP$-complete, it's very unlikely there's a polynomial time algorithm.

What is the space complexity of this algorithm?

PSPACE

As a counterpart to the class $P$, which is the class of problems solvable in polynomial time, we define $PSPACE$ as the class of problems which are solvable in polynomial space:

$PSPACE = \bigcup\limits_{k} SPACE(n^k)$

$PSPACE$ is the class of problems for which there exists a Turing machine whose space complexity is any polynomial function.

Because $SAT$ is solvable in polynomial space, $SAT \in PSPACE$.

NPSPACE

Likewise we can define the class $NPSPACE$ as the set of problems which can be solved in polynomial space on a non-deterministic Turing machine. As with time, the space complexity of a non-deterministic Turing machine is the maximum space used on any branch of computation. This is also the class of problems which can be verified in polynomial time.

$NPSPACE = \bigcup\limits_{k} NSPACE(n^k)$

$NPSPACE$ is the class of problems for which there exists a non-deterministic Turing machine whose space complexity is any polynomial function.

Savitch's Theorem

Savitch's theorem states that $PSPACE$ is exactly equal to $NPSPACE$.

This is very different from the $P$ vs. $NP$ situation where it is unknown if the two classes are equal (and most people would guess they are unequal).

The proof of Savitch's theorem is based on showing that a non-deterministic Turing machine can be simulated by a deterministic one with only a quadratic increase in space needed.

If a non-deterministic Turing machine runs in $f(n)$ space, a deterministic one can be built which runs in $f(n)^2$ space. Because any polynomial squared is still a polynomial, any problem which is in $NPSPACE$ is also in $PSPACE$.

Relationship Between Time and Space Complexity

What is the relationship between these space complexity classes and the time classes $P$ and $NP$?

The class $P$ is a subset of $PSPACE$ for the simple reason that if an algorithm only takes polynomial time, it simply doesn't have a chance to access more than a polynomial number of tape cells.

Likewise, class $NP$ is a subset of class $NPSPACE$ because a non-deterministic Turing machine can't access more than a polynomial amount of cells in a polynomial amount of time. Because $PSPACE = NPSPACE$, $NP$ is a subset of $PSPACE$ as well.

This may seem counter-intuitive, that the very hard problems in $NP$ can always be solved in polynomial space, but the $SAT$ problem provides an example of this. As we saw earlier, it runs in linear space so it is a member of $PSPACE$. Recall that $SAT$ is $NP$-complete, so it is one of the hardest problems in $NP$.

In a sense, time is a more "scarce" resource than space because time cannot be reused while space can.

The figure below represents these relationships:

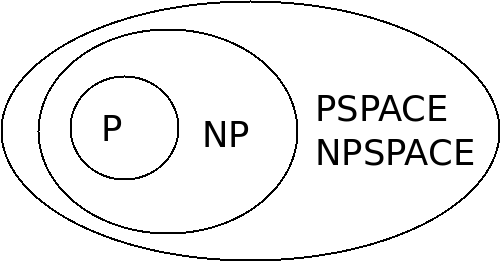
It is strongly suspected that each of these is a proper subset, but it has not been proven.

PSPACE-Completeness

Just like we have the $NP$-complete problems, which are the hardest ones in $NP$, which are likely not in $P$, we will define $PSPACE$-complete problems as those which are the hardest ones in $PSPACE$, and not likely to be in $NP$.

For a language $A$ to be $PSPACE$-complete, it must satisfy the following:

$A$ must be in $PSPACE$.
Every problem in $PSPACE$ must be reducible to $A$ in a polynomial amount of time.

The TQBF Problem

The True Quantified Boolean Formula problem is an extension of the $SAT$ problem where we introduce the universal and existential quantifiers ($\forall, \exists$).

An example of a quantified boolean formula is:

$\forall x\ \exists y\ ( (x \vee y) \wedge (\overline{x} \vee \overline{y}) )$

Is this formula true or false?

What if we swap the quantifiers?

The $TQBF$ is to decide whether a quantified boolean formula is true or not.

This is a harder problem than $SAT$ problem, as it is suspected to not belong in $NP$ at all. There is no known way to verify whether a quantified formula is true, even if we are allowed to create a "certificate" representing a potential answer.

The problem is decidable, however, and the following algorithm decides it:

$T = $ "On input $\phi$, a quantified boolean formula:

If $\phi$ contains no quantifiers, then it contains only constants. Evaluate the formula and accept if true, but reject if false.
If $\phi$ matches the form $\exists x\ \psi$, then recursively run $T$ on $\psi$, first with $x$ set to false, then with $x$ set to true. If either accepts, then accept. Otherwise reject.
If $\phi$ matches the form $\forall x\ \psi$, then recursively run $T$ on $\psi$, first with $x$ set to false, then with $x$ set to true. If both accepts, then accept. Otherwise reject."

What are the space and time complexity of this algorithm?

It has been proven that all problems in $PSPACE$ can be reduced to $TQBF$ in a polynomial amount of time, similarly to how the Cook-Levin theorem proves that all problems in $NP$ can be reduced to $SAT$ in a polynomial amount of time.

Conclusion

Space complexity provides another way to classify difficult problems. Many more problems can be solved efficiently with regards to space than time (because unlike time, space can be reused).

There is a link between time complexity and space complexity in that any problem in $P$ or $NP$ takes no more than a polynomial amount of time. However, some problems such as $TQBF$ and the problem of picking winning moves in certain games cannot even have solutions verified in polynomial time.