Problems which are $NP$-complete are the hardest problems in $NP$. If a problem is $NP$-complete, then a solution to it would provide a solution to all other problems in $NP$. No efficient (polynomial time) solution is known to any of these.
We have seen a few $NP$-complete problems already:
Today we will look at a few more.
If $G$ is an undirected graph, a vertex cover of $G$ is a subset of the nodes where every edge in $G$ touches one of the nodes. The vertex cover problem asks whether a graph contains a vertex cover of a certain size, $k$.
How can we show that this problem is in $NP$?
A solution to this problem also can be used to solve $3SAT$. The reduction constructs a graph using the following algorithm:
Below is a graph constructed for the formula $(x_1 \vee x_1 \vee x_2) \wedge (\overline{x_1} \vee \overline{x_2} \vee \overline{x_ 2}) \wedge (\overline{x_1} \vee x_2 \vee x_2)$:
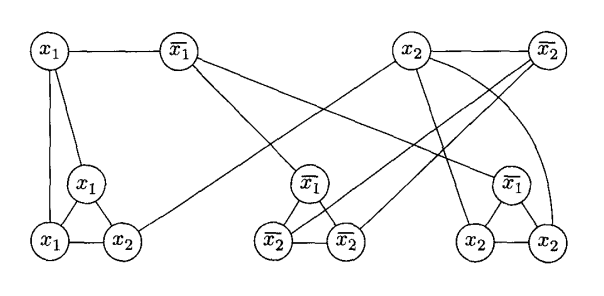
Choose $k$, the size of the vertex cover to be $m + 2l$ where $m$ is the number of variables, and $l$ is the number of clauses. $k$ is 8 in the example above.
A solution to this instance of the vertex cover problem will provide a solution to the corresponding instance of the $3SAT$ problem because we are forced to choose one of the nodes in each variable pair, and two in each clause to get to $k$ nodes with each edge covered.
For the above example, what nodes would we have to choose to solve $VC$, and how does that correspond to the original $3SAT$ problem?
Because $3SAT$ can be polynomially reduced to the vertex cover problem, then the vertex cover problem is also $NP$-complete.
The Subset Sum problem can be stated as:
Given a set of integers, is there a non-empty subset whose sum is some constant $t$?
Can this be done with the following numbers where $t = 0$?
31 -42 -20 -80 82 -62 -62 83 -24 18 92 -94 -49 91 -45 10 -12 -75 83 31 -62 48
How can we show that this problem is in $NP$?
This problem also can be shown to be $NP$-complete via a reduction from $3SAT$. Here, we need to show that an instance of the $3SAT$ problem can be solved via converting it into an instance of the subset sum problem.
Imagine again that we have the following $3SAT$ problem:
$(x_1 \vee x_1 \vee x_2) \wedge (\overline{x_1} \vee \overline{x_2} \vee \overline{x_2}) \wedge (\overline{x_1} \vee x_2 \vee x_2)$
We will build a table of (large) values such that a certain sum from the values can be obtained when, and only when, the $3SAT$ problem has a satisfying assignment.
We will create $y_i$ which is 1 when $x_i$ is true, and $z_i$ which is 1 when $x_i$ is false. We will create our list of numbers such that one or the other must be selected for each $x_i$. This will ensure that each variable is either true or false.
We also must ensure that at least one term from each of the clauses is true. To do this, we will have one column of each number reserved for each clause. That column will contain a 1 digit when the corresponding $y_i$ or $z_i$ is true. When setting the number $t$ (the desired sum), we will force at least one from each clause to be true.
The last idea in this construction is to allow two extra digits to be selected for each clause. The purpose of these (labelled $g_i$ and $h_i$ below) is to allow us to have more than one piece of each clause come out true. We do this by requiring a value of 3 for each clause. If all three pieces are true, we need nothing else. If only 1 or 2 of the pieces are true, we select 1 or 2 of the additional numbers to get up to 3.
Below is the table of numbers which corresponds to the $3SAT$ instance above:
| $c_1$ | $c_2$ | $c_3$ | |||
| $y_1$ | 1 |
0 | 1 | 0 | 0 |
| $z_1$ | 1 | 0 | 0 | 1 | 1 |
| $y_2$ | 0 | 1 | 1 | 0 | 1 |
| $z_2$ | 0 | 1 | 0 | 1 | 0 |
| $g_1$ | 0 | 0 | 1 | 0 | 0 |
| $h_1$ | 0 | 0 | 1 | 0 | 0 |
| $g_2$ | 0 | 0 | 0 | 1 | 0 |
| $h_2$ | 0 | 0 | 0 | 1 | 0 |
| $g_3$ | 0 | 0 | 0 | 0 | 1 |
| $h_3$ | 0 | 0 | 0 | 0 | 1 |
| $t$ | 1 | 1 | 3 | 3 | 3 |
The only way to sum the table of numbers to the value $t$ is to select exactly one of each $y_i$ or $z_i$ values for each $i$ (or else we would not get 1 for each variable column). This will also select those bits in the $c_i$ columns. Each clause must have at least one '1' chosen amongst the $y_i$ or $z_i$ lines. That means at least one of its terms was chosen to be true. The $g$ and $h$ lines can then be added in to get up to 3.
Finding a sum of $t$ amongst these numbers would provide us with a solution to the corresponding $3SAT$ problem. Thus $3SAT$ reduces to subset sum. If we could quickly solve subset sum problems, then we could quickly solve $3SAT$ problems as well. Therefore the subset sum problem is also $NP-complete$.
The graph coloring problem can be stated as:
Given a graph $G$, and an integer $k$, is it possible to color the nodes of $G$ in $k$ colors, such that no edge connects two nodes with the same color.
Below is a graph with the minimum number of colors:
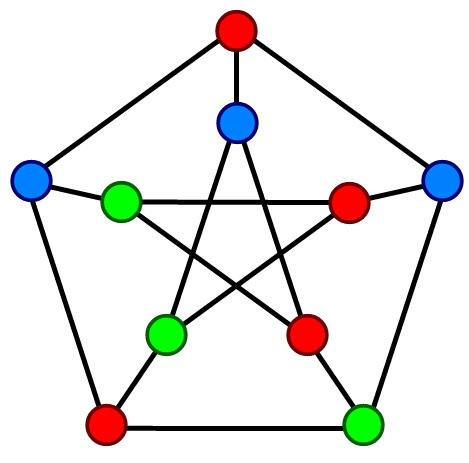
How many ways are there to color a graph with $N$ nodes and $k$ colors?
This problem has applications in scheduling and register allocation.
The Knapsack problem can be stated as:
Given a set of items which each have some weight and some value, how could we pack a knapsack with items such that it has the highest total value without exceeding a maximum weight?
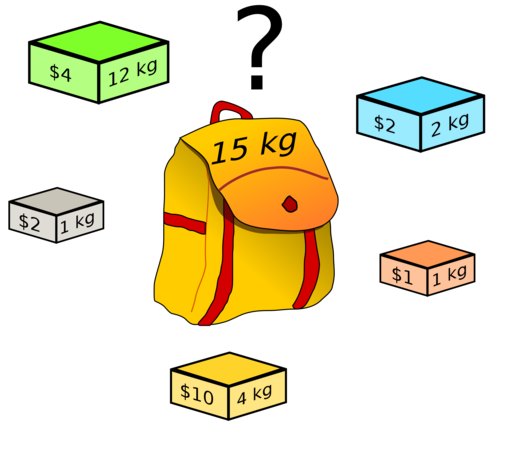
How many different ways could we choose to pack the knapsack if we have $N$ items?
This problem shows up in numerous places where we want to optimize some set of choices where there are costs and gains associated with each option.
The bin packing problem can be stated as:
Given a set of objects with different volumes, and a number $k$ of "bins" of a fixed size, is it possible to pack all of the items into $k$ bins?
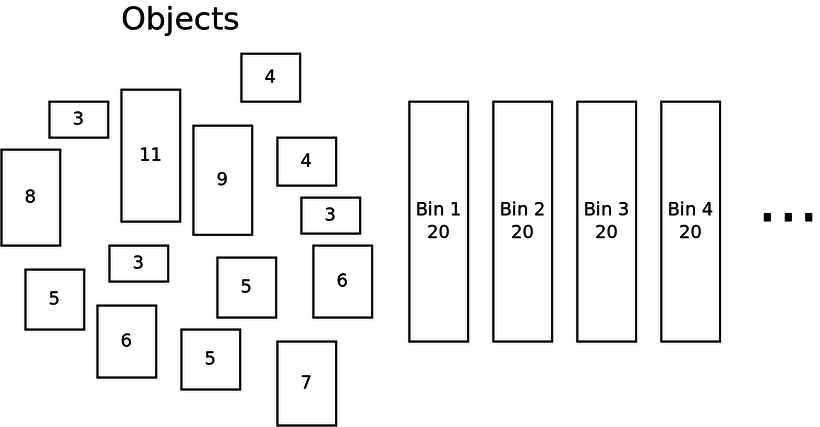
How many bins are needed to pack the items above?
How many ways could we try to pack $N$ items into $k$ bins?
This problem has applications in shipping and storage of goods, and the optimal layout of data in memory.
In this problem, we are given a set of sequences and need to find the longest chain that they have in common.
In the following two sequences of numbers, what is the longest subsequence which they share?
1 22 46 68 28 34 65 30 38 14 45 15 91 43 65 9 22 46 68 91 43 65 30 38 14 45 15 2 8 87 27 60
This problem has applications in data compression, file comparisons and bioinformatics.
Because all of these problems are essentially unsolvable in a reasonable amount of time for sufficiently large input sizes, but we do actually need solutions for some of them, we have to settle for approximations.
An approximation algorithm is one that does not actually give you an answer, but gives you as close to an answer as it can. For instance, in graph coloring applications, we want the minimum number of colors. An approximation algorithm tries to give the smallest number it can, but does not guarantee the result is actually minimal.
There are a few general approaches to approximation algorithms:
Greedy Algorithms
Greedy algorithms are those which build a solution step by step, where we take the "next best" option at each step. How could we build greedy algorithms for the problems above?
Local Search
Local search algorithms start with a candidate solution and change it in such a way that it becomes more optimal, and stop when it becomes less optimal. The result might not be the (global) best answer, but it is the best answer locally.
Randomized Algorithms
A randomized algorithm is one where we try random solutions to the problem, and keep the best solution that we randomly generate. A special case of this is "genetic algorithms" which combines the best solutions to try to "evolve" the best possible answer.
Upon devising an approximation algorithm, we may ask whether we can prove anything about how close to optimal its results are. For instance some approximation algorithms can be guaranteed to produce results no worse than constant factor away from the best solution.
Though we did not show it, each of these $NP$-complete problems has been shown to be fulfill the property that any problem in $NP$ can be reduced to it in polynomial time.
This means that if any polynomial time algorithm for any of these problems is found, then we will have polynomial time algorithms for every problem in $NP$.
$NP$-completeness is an important concept both theoretically and practically. Theoretically, they represent the most difficult problems in $NP$. The ones that are suspected to belong to $NP$ but not $P$.
Practically, $NP$-completeness is important because it represents the set of problems that have no known polynomial time solution. If you are presented with a problem that is $NP$-complete, you probably will not be able to solve it for large input sizes.
Copyright © 2024 Ian Finlayson | Licensed under a Creative Commons BY-NC-SA 4.0 License.