The Class NP

Overview

$P$ is the class of problems that have polynomial time solutions. Generally $P$ is the set of problems with efficient solutions - ones that do not rely on "brute force".

There are some problems that have no known polynomial time solutions. The only known solutions are to try essentially every possible solution. Many of these problems belong to a class called $NP$.

The Hamiltonian Path Problem

A Hamiltonian path is a path through a graph which visits every node exactly once. The Hamiltonian path problem is that of deciding whether or not a graph has a Hamiltonian path:

$HAMPATH = \{\langle G, s, t \rangle\; |\; G$ is a directed graph with a Hamiltonian path from $s$ to $t\}$

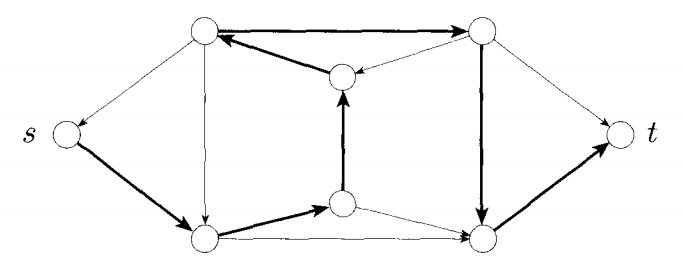
No polynomial time solution for $HAMPATH$ is known, it is an example of a problem in $NP$, but not known to be in $P$. What solution could we use to solve the problem in more than polynomial time?

Verifiers

While there is no known algorithm to decide $HAMPATH$, we can verify a potential solutions to it in polynomial time. If we had a possible solution to $HAMPATH$, how could we verify that it was, in fact, a Hamiltonian path?

We say a verifier $V$ verifies some language $A$ if:

$A = \{w\; |\; V \text{ accepts } \langle w, c \rangle \text{ for some string } c\}$.

$c$ is sometimes called a certificate. Given the certificate, the verifier determines if it does in fact solve the problem.

In the Hamiltonian path example, the string $w$ is the instance of the problem $\langle G, s, t\rangle$. $c$ is the possible solution: an encoding of a path through $G$. $V$ is the verifier: an algorithm which checks if the path $c$ is Hamiltonian. $A$ is the language $HAMPATH$ itself.

Definition of NP

$NP$ is defined as the class of problems that have polynomial time verifiers. Because $HAMPATH$ can be verified in polynomial time, it belongs to $NP$.

This definition of $NP$ also includes all of $P$. Every problem in $P$, has a polynomial time verifier. The verifier can work by simply ignoring the certificate, deciding the problem itself, in polynomial time, and using that as its answer.

Thus, $P \subseteq NP$.

NP And Non-Determinism

An alternate way of defining $NP$ is as the set of problems that can be solved using polynomial time on a non-deterministic Turing machine.

In fact, $NP$ actually stands for "Non-deterministic Polynomial". It does not stand for "non-polynomial" since it is not known whether problems such as $HAMPATH$ are in $P$ or not.

Below is a non-deterministic Turing machine $N_1$ which decides $HAMPATH$:

$N_1 =$ "On input $\langle G, s, t\rangle$:

Write a list of $m$ numbers $p_1, p_2...p_m$ where $m$ is the number of nodes in $G$. Each number is non-deterministically chosen and is between 1 and $m$.
Check for repetitions in the list. If there are any, reject.
Check that $s = p_1$ and $t = p_m$. If not, reject.
For each edge $i$ between $1$ and $m - 1$, check that $(p_i, p_{i+1})$ is an edge of $G$. If any are not, reject.
If all tests pass, accept.

What complexity does this algorithm run in?

We can always construct a non-deterministic Turing machine to decide a problem in $NP$ using the following outline:

Non-deterministically choose a certificate $c$.
Run the verifier on $c$.

Step 1 will take polynomial time because the certificate must be polynomial in length (otherwise the verifier - which we know is polynomial - could not even read it all). Step 2 is also polynomial because the verifier is polynomial.

The Composite Problem

Another problem in $NP$:

$COMPOSITES = \{x\; |\; x = p \times q, \text{ for integers } p, q > 1\}$

In this problem we are given an integer and want to know if it is a composite number, that is whether it is prime or not.

How can we show that this problem is in $NP$?

The Clique Problem

Another example of a problem in $NP$ is the clique problem. A clique is a fully-connected sub-graph within a graph. A $k$-clique is a clique with $k$ nodes.

jp>The following graph has a 5-clique:

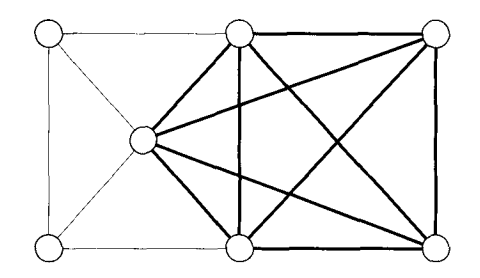
We can state the clique problem as:

$CLIQUE = \{\langle G, k \rangle\; |\; G \text{ is an undirected graph with a } k\text{-clique}\}$.

How can we show that this problem is in $NP$?

P Versus NP

$NP$ is the set of problems that can be verified in polynomial time. $P$ is the set of problems that can be solved in polynomial time.

$HAMPATH$ and $CLIQUE$ are both in $NP$. It is not known whether they belong to $P$ as well.

No efficient algorithm for these problems is known, but the non-existence of such an algorithm has never been proved either.

One of these two diagrams represents the relationship between $P$ and $NP$:

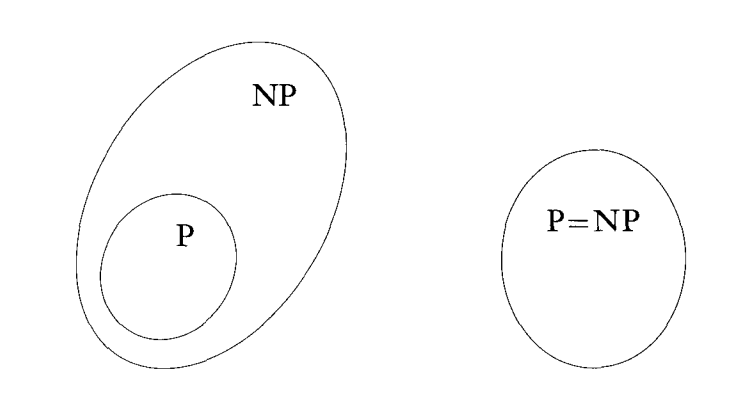
Most people believe the left diagram is correct. This is the greatest unsolved problem in computer science.