Turing Machines

Overview

We have seen the limits of regular and context-free languages. Today we will look at a more powerful type of automata, the Turing machine, which can recognize some languages that are not regular or context-free.

Description

Like a PDA, a Turing machine has an unlimited memory. However, it is able to read and write any portion of it, at any time.

The memory is called a "tape". Initially, the tape begins with the input string stored on it. The tape extends infinitely to the right. Tape locations past the input length are initialized with the blank symbol: $\sqcup$

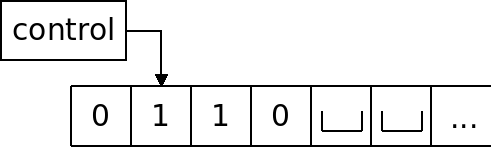
Turing machines are able to do any of the following operations:

Read from the tape.
Write to the tape.
Move the tape head to the left.
Move the tape head to the right.

Example

The following language is not regular, and also not context-free: $\{w\#w \ |\ w \in \{0, 1\}^\ast\}$.

How would a Turing machine that recognizes this language operate?

Formal Definition

Formally, a Turing machine is defined as:

$Q$, the set of states.
$\Sigma$, the input alphabet not containing the blank symbol, $\sqcup$.
$\Gamma$, the tape alphabet, where $\sqcup \in \Gamma$ and $\Sigma \subseteq \Gamma$.
$\delta : Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}$ is the transition function.
$q_0 \in Q$, is the start state.
$q_{accept} \in Q$ is the accept state.
$q_{reject} \in Q$ is the reject state, where $q_{accept} \neq q_{reject}$.

The transition function input is the current state, and tape symbol under the read head. The output is the next state, the symbol to write, and either $L$ or $R$, which indicates that we move the head left or right.

The accept and reject states take effect immediately in a Turing machine.

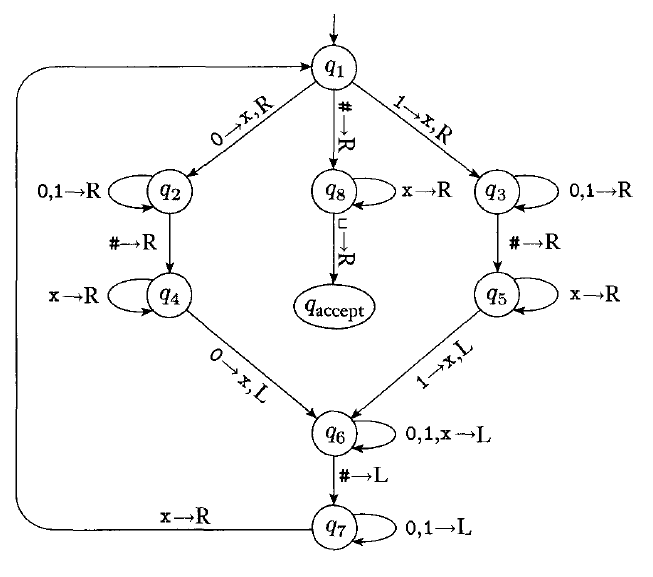
Example

Below is a diagram of the Turing machine which recognizes $\{w\#w \ |\ w \in \{0, 1\}^\ast\}$:

Turing-Recognizable Languages

Like other automata, we say that the collection of strings which a Turing machine $M$ accepts is the language of $M$, denoted as $L(M)$.

A language is Turing-recognizable if some Turing machine recognizes it.

Decidable Languages

With a DFA, NFA, or PDA, the automata will always stop at some point. This is not true of a Turing machine. With a Turing machine, it's possible to create infinite loops.

With a Turing machine, there are three possible outcomes:

The machine accepts.
The machine rejects.
The machine runs forever never accepting or rejecting.

If a Turing machine always halts, no matter the input, it is a decider. The language of a decider is decidable language.

Some languages are Turing-recognizable but not decidable.

On Formal Descriptions

Describing a Turing machine in detail, as in the example above, is usually too tedious for complex languages.

Instead, we will describe the behavior of the machine informally. The Turing machine above can be described as follows:

$M_1 = $ "On input string $w$:

Zig-zag across the tape to corresponding positions on either side of the # symbol to check whether those positions contain the same symbol. If they do not, or no # is found, reject. Cross off symbols to keep track of which symbols correspond.
When all symbols to the left of the # have been crossed off, check for any remaining symbols to the right of the #. If any remain, reject; otherwise, accept."

These descriptions must be sufficiently detailed that we can envision exactly the steps the Turing machine will take.

Is this Turing machine a decider?