Context-Free Grammars

Overview

Regular languages are powerful enough to express many things, but we've shown there are languages that are not regular. For example:

$\{0^n1^n \;|\; n \geq 0\}$

Is not a regular language.

This language is, however, a context-free language.

Context-free languages are capable of expressing more complex patterns. Context-free languages include most programming languages.

Context-Free Grammars

Context-free grammars are a textual way of describing a context-free language.

Below is a context-free grammar for the language above:

$A \rightarrow 0A1$

$A \rightarrow B$

$B \rightarrow \epsilon$

A CFG is comprised of the following:

Variables

These are symbols that may be substituted for strings of other variables or terminals. $A$ and $B$ are the variables in the above grammar.
Terminals
Terminals are the symbols that comprise the alphabet of the language we are describing. $0$, $1$, and $\epsilon$ are the terminals above.
Productions
Productions (or rules) define the substitutions that are permitted in the grammar. A production consists of a left hand side, and arrow, and a right hand side. The left hand side must be a single variable, and the right can be any string of variables and terminals. There are three productions above.
A start variable
The start variable is the one that we begin the derivation process with. It is typically the left hand side of the first production. $A$ is the start variable above.

Derivations

Context-free grammars produce strings that belong to the language they describe. The production of a string is called a derivation:

Start with the string equal to the start variable.
Find a variable in the string, and a production with that variable as the left hand side. Replace the variable with the right hand side of the production.
Repeat step 2 until no variables remain.

How could we derive "000111" according to the CFG above?

The set of all strings a grammar $G$ can produce is called the language of that grammar and is written as $L(G)$.

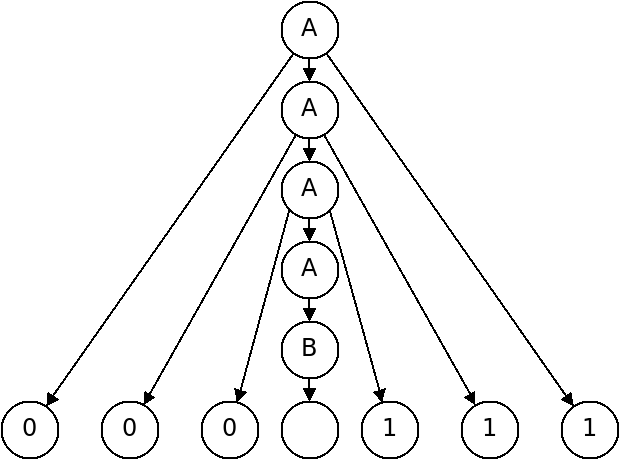
Parse Trees

Another way of depicting a derivation is with a parse tree.

In a parse tree, we start with one node for the start variable - the root of the tree. Each time we follow a production, we make children nodes for each symbol on the right hand side. In the completed parse tree, the terminals are the leaf nodes.

Below is a parse tree for the string "000111":

Language Example

Below is a CFG which describes a fragment of the English language:

How can we derive:

a boy sees
the girl sees a flower
a girl with a flower likes the boy

Formal Definition

A context-free grammar is defined by the following four things:

$V$, the finite set of variables.
$\Sigma$, the finite set, disjoint from $V$, of terminals.
$R$ is a finite set of rules, with each rule having a variable and a string of variables and terminals.
$S \in V$ is the start variable.

For convenience we allow multiple productions with the same left hand side to be collapsed. For example:

$A \rightarrow 0A1$

$A \rightarrow B$

Could instead be written as:

$A \rightarrow 0A1 \ |\ B$

When analyzing the grammar, however, this counts as two productions.

Building Grammars

Like automata or regexes, designing CFGs requires creativity. How can we build a CFG for the language $\{w \;|\; w$ starts and ends with the same symbol$\}$?

A Grammar for Arithmetic

The following CFG attempts to recognize well-formed arithmetic expressions involving addition, subtraction, multiplication and division:

$\langle expr\rangle \rightarrow \langle expr\rangle \langle op\rangle \langle expr\rangle \ |\ ( \langle expr\rangle ) \ |\ number$

$\langle op\rangle \rightarrow + \ |\ - \ |\ * \ |\ /$

How can we produce the following strings with this grammar:

$6 * 7$
$3 + (4 / 7)$
$1 + 2 + 3$

Ambiguity

This grammar will distinguish well-formed strings from bad ones, but it is not helpful in capturing the structure of strings because it is ambiguous.

For a string such as $3 + 4 * 5$, there are multiple different ways to derive it:

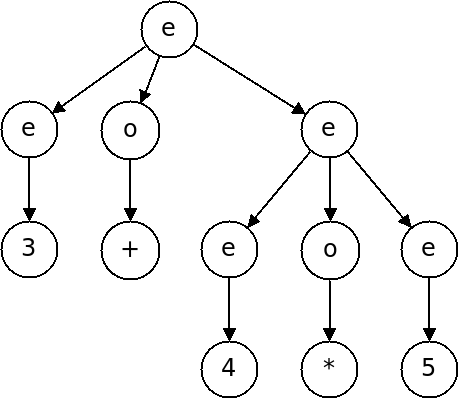
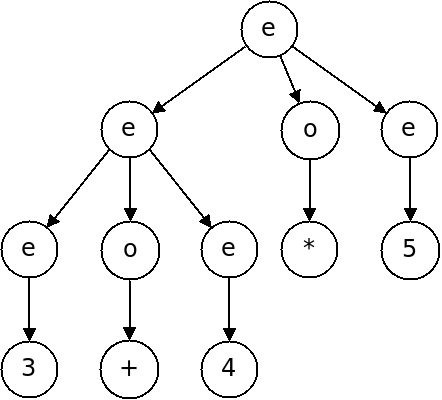
Which of these two is correct?

A grammar is ambiguous if there are two distinct parse trees for the same string, that are both correct in the grammar.

Ambiguity of Natural Language

The grammar which forms a subset of the English language is below.

This grammar is ambiguous as well. Which two ways can we derive:

the girl touches the boy with the flower

Which of these two is correct?

Unlike artificial languages, ambiguity in natural language is something we must accept.

Disambiguating Arithmetic

There is no set procedure for removing ambiguity from a grammar. We must construct the grammar in such a way so that it forces a derivation to proceed in the way we want.

Below is an improved grammar for arithmetic expressions which forces multiplication and division to have a higher precedence than addition and subtraction:

$\langle expr\rangle \rightarrow \langle expr\rangle \langle addop\rangle \langle term\rangle \ |\ \langle term\rangle $

$\langle term\rangle \rightarrow \langle term\rangle \langle multop\rangle \langle factor\rangle \ |\ \langle factor\rangle $

$\langle factor\rangle \rightarrow number \ |\ ( \langle expr\rangle )$

$\langle addop\rangle \rightarrow + \ |\ -$

$\langle multop\rangle \rightarrow * \ |\ /$

Now what parse tree is produced for $3 + 4 * 5$?

Applications of Context-Free Grammars

CFG's are widely used to describe artificial languages including arithmetical expressions, but also complete programming languages (here is a grammar for Python). There are even ways of converting a grammar into a program which decides if strings belong to the language or not.