Home CPSC 326
Contents ▼
Overview The Pumping Lemma Pumping Lemma Explanation Pumping Example Proving Non-Regularity Example Proving Regularity/Non-Regularity

Non-Regular Languages

 

Overview

We've seen several ways of representing regular languages:

We can lots of interesting things with regular languages, but there are many languages that are not regular:

These languages have no finite automata which recognizes them, and no regular expression which generates them.

Today we will look at how we can show that a language is not regular.

 

The Pumping Lemma

The pumping lemma states that all regular languages have a certain property. If we can show that a language does not have that property, then it must not be regular.

The pumping lemma states:

If $A$ is a regular language, then there is a number $p$ where if $s$ is any string in $A$ of length at least $p$, then $s$ may be divided into three pieces $s = xyz$ satisfying the following:

  1. $\forall i \geq 0, xy^iz \in A$
  2. $|y| > 0$
  3. $|xy| \leq p$
 

Pumping Lemma Explanation

If $A$ is a regular language, then we know some DFA $M$ recognizes it. We can assign $p$ to be the number of states of $M$.

We then choose any string $s$ that is part of $A$ and has length at least $p$.

We then look at the states that $M$ is in as it computes $s$. It will visit exactly $n + 1$ states, when $n$ is the length of $s$:

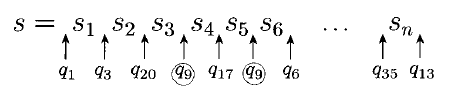
By the pigeonhole principle, we must visit some state twice!

The part of s that comes before the repeated state is $x$. The part between is $y$. The part after is $z$.

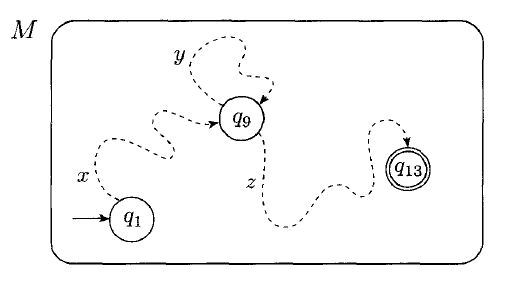
This satisfies the three conditions:

  1. No matter how many times we loop $y$, we will still have a string in $A$.
  2. The string $y$ is not empty.
  3. $xy$ cannot be greater than $p$, the number of states (else there would be another repetition).

The big idea here is that with a finite number of states, a DFA cannot produce strings of arbitrary length without at some point returning to the exact same state it had been at previously.

 

Pumping Example

How can we demonstrate the pumping lemma for the language generated by $01^\ast0$?

 

Proving Non-Regularity

The main use of the pumping lemma is to prove that languages are not regular. The basic idea is this:

Given a language $L$ we suspect to be non-regular,

  1. Assume $L$ is regular, and that the pumping lemma holds.
  2. Show that, for some choice of $p$ and $s$, the pumping lemma does not hold.
  3. Conclude that the assumption of the regularity of $L$ was not true.

Note that, the pumping lemma holds for any choice of $p$ or $s$. A non-regular language may well have some strings in it that can be pumped!

 

Example

Let $B = \{0^n1^n \ |\ n \geq 0\}$

  1. Assume $B$ is regular.
  2. Choose $s = 0^p1^p$. Because $s$ is a member of $B$, and $|s| \geq p$, the pumping lemma says we can split $s = xyz$ and that $\forall i \geq 0 xy^iz \in A$.

There are three cases for our choice of $y$:

  1. $y$ consists entirely of zeroes. In this case, $xyyz$ will have more zeroes than ones and will no longer be a member of $B$.
  2. Likewise, if $y$ contains only ones, looping it will produce strings with more ones than zeroes.
  3. $y$ contains some zeroes and some ones. In this case $xyyz$ may have an equal number of zeroes and ones, but they will be out of order.

No matter the choice of $y$, we cannot pump $y$ without leading us to strings which are not part of our language.

Therefore the pumping lemma does not hold for $B$ and it must be non-regular.

 

Proving Regularity/Non-Regularity