Regular Expressions Continued

Finite Automata $\rightarrow$ Regular Expression

We have shown that any regular expression can be converted into a finite automata. Now we will prove the opposite, that any finite automata can be converted into a regular expression.

First we will need a new type of finite automata, the Generalized Nondeterministic Finite Automata.

GNFAs

A GNFA is an NFA where each transition can have arbitrary regular expressions as labels rather than just elements of $\Sigma$.

GNFAs can consume multiple input symbols on each transition.

We also require GNFAs follow these rules:

The start state has a transition going to every other state, but no transitions into it.
There is a single accept state, and every state transitions to it, but it doesn't transition to any state.
Except for the start and accept state, each other state has transitions to every other state (including itself).

These rules will make the conversion simpler.

DFA $\rightarrow$ GNFA Conversion

To convert a DFA into a GNFA we follow these steps:

Add a new start state with an $\epsilon$-transition to the old start state.
Add a new accept state with $\epsilon$-transitions from each old accept state.
If any transitions have multiple symbols, merge them with a union.
If there are transitions missing, create transitions with $\emptyset$ as the label.

Conversion Example

How would we convert the following DFA into a GNFA?

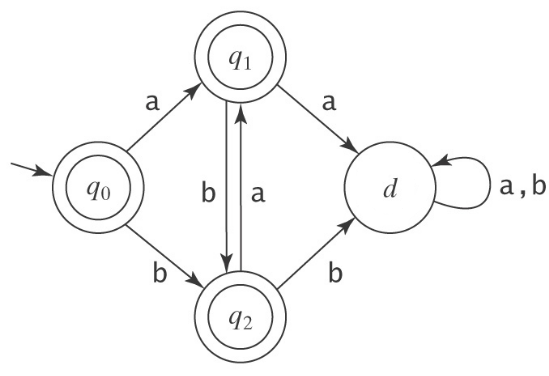
GNFA $\rightarrow$ Regular Expression Conversion

Now we need to convert the GNFA into a Regular Expression.

This is done by removing the states of the GNFA one at a time until only the start and accept states remain. The label on the transition from the start state to the accept state will be our regular expression:

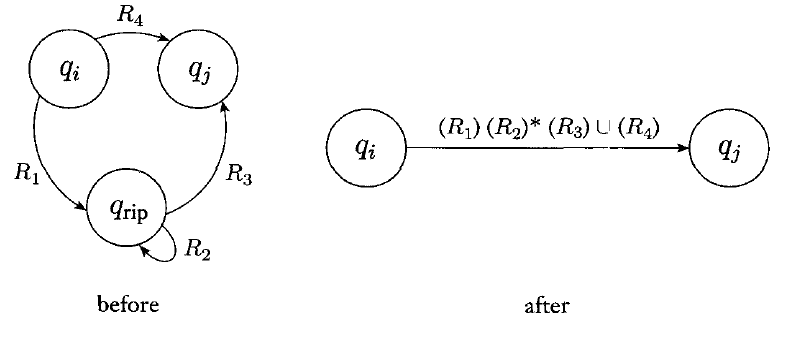
We can do this by choosing any state, ripping it out, then repairing the transitions so that the machine functions the same as before.

Formally: we can define a GNFA as:

$Q$ is the set of states.
$\Sigma$ is the alphabet.
$\delta: (Q - \{q_{accept}\}) \times (Q - \{q_{start}\}) \rightarrow R$ is the transition function.
$q_{start}$ is the start state.
$q_{accept}$ is the accept state.

Given a GNFA $G$, we can produce an equivalent one with one fewer state, called $G^\prime$ using this procedure:

Select a state $q_{rip} \in (Q - \{q_{accept}, q_{start}\})$.
$Q^\prime = Q - \{q_{rip}\}$.
For any $q_i \in (Q^\prime - \{q_{accept}\})$ and any $q_j \in (Q^\prime - \{q_{start}\})$, let

$\delta^\prime(q_i, q_j) = (R_1)(R_2)^\ast(R_3) \cup (R_4)$, where

$R_1 = \delta(q_i, q_{rip})$,
$R_2 = \delta(q_{rip}, q_{rip})$,
$R_3 = \delta(q_{rip}, q_j)$,
$R_4 = \delta(q_i, q_j)$

Below is an illustration:

Conversion Example

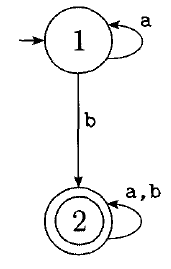
How could we convert this DFA into a regular expression?

Conversion Example 2

How could we take this more complex DFA all the way to a regular expression?

Regular Languages

We now have three ways to talk about regular languages:

DFAs
NFAs
Regular Expressions

All three are equivalent.

Next we will discuss languages that are not regular and thus have no finite automata recognizing them, or regular expression producing them.