DFA-NFA Equivalence

Equivalence Between NFAs and DFAs

NFAs and DFAs both recognize the same class of languages, regular languages. In other words, there is no language for which we can build an NFA but not a DFA.

To prove this is the case, we will need to show that every NFA can be converted into an equivalent DFA.

The main idea is that, given some NFA, we will construct from it a DFA which simulates the NFA, accepting when it accepts and rejecting when it rejects.

What do we need to keep track of when simulating an NFA?

Equivalence Proof

Let $N = (Q, \Sigma, \delta, q_{0}, F)$ be the NFA recognizing some language $A$. We construct a DFA $M = (Q^\prime, \Sigma, \delta^\prime, q_{0}^\prime, F^\prime)$ recognizing the same language $A$.

For now, we discount the possibility of $\epsilon$ transitions.

$Q^\prime = \mathcal P(Q)$.
Every state of M is a set of states in N. Recall that $\mathcal P(Q)$ is the power set of $Q$.
$q_{0}^\prime = \{q_{0}\}$.
The start state of M is the state corresponding to the set of states containing only the start state of N.
$F^\prime = \{R \in Q^\prime \;|\; R \text{ contains an accept state of N}\}$.
The accept states of M are all those states containing an accept state of N.
$\text{For } R \in Q^\prime \text{ and } a \in \Sigma \text{ let } \delta^\prime(R, a) = \{q \in Q \;|\; q \in \delta(r, a) \text{ for some } r \in R\}$.
Our transition function takes a set of states of the NFA, and an input. The output is the set of states of the NFA which contains any state that we can reach from those states in the NFA on that input.

Basically, the DFA we build has a state for every possible combination of states the NFA could be in. As it reads input, it essentially simulates all paths through the NFA concurrently.

$\epsilon$ Transitions

In order to handle these, there is an extra bit of notation:

Given that $R$ is a set of states, let

$E(R) = \{q \;|\; q \text{ can be reached from R by traveling along 0 or more } \epsilon \text{ arrows}\}$

Then we modify the transition function of M to add in the states we can reach by $\epsilon$-transitions after each step:

$\delta(R, a) = \{q \in Q \;|\; q \in E(\delta(r, a)) \text{ for some } r \in R\}$.

The transition function basically works by looking at the set of states we are currently in ($R$), and finding every state we could get to from this state, given the input ($a$), in the NFA, and where we can then go via $\epsilon$-transitions.

We also must modify the start state to include $\epsilon$-transitions from the start state:

$q_{0}^\prime = E(q_{0})$

Using this algorithm, we can construct an equivalent DFA for any NFA. Thus, any language that has an NFA which recognizes it is regular.

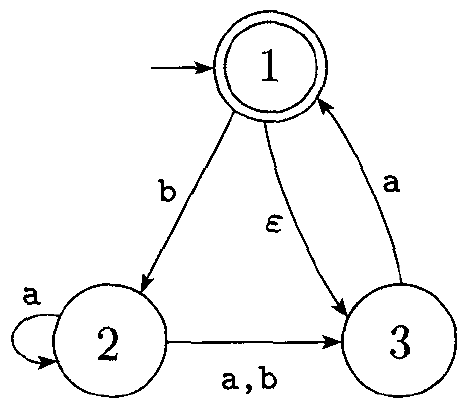
Conversion Example

How could we convert the following NFA into a DFA, using the above procedure?