More Deterministic Finite Automata

Operations on Regular Languages

Because languages are sets, and regular languages are a type of language, we can perform set operations on regular languages. These operations allow us to create new languages from existing ones.

Today we will look at some set operations as applied to regular languages, and consider whether regular languages are closed under these operations.

Closure

The term closure refers to whether operations on something always produce the same sort of thing.

For instance integers are closed under multiplication because if we multiply two integers together, we always get another integer. However integers are not closed under division because we sometimes when we divide two integers, the result is not an integer.

When we say that regular languages are closed under some operation, we mean that the operation will always produce another regular language as the result.

Complement

The complement of a language $L$ (often written as $\overline{L}$) is the set of all strings not in $L$. For example:

$L = \{w \ |\ w \text{ contains 001}\}$
$\overline{L} = \{w \ |\ w \text{ does not contain 001}\}$

Given any regular language $L$, is its complement also guaranteed to be a regular language?

Yes:

Because $L$ is a regular, there is a DFA, $M$, which recognizes $L$.
We can construct a new DFA $M'$ by copying $M$, and replacing $F$, the set of accept states with $\overline{F}$.
This machine recognizes $\overline{L}$.
Because a DFA recognizes $\overline{L}$, it is regular.

This proof by construction shows that we can construct a DFA to recognize the complement of any regular language. Therefore the complement of any regular language is also regular, so the class of Regular Languages are closed under complement.

Union

$A \cup B = \{x \ |\ x \in A$ or $x \in B\}$

The union of two languages is simply the set of words that belong to either one language or the other (or both).

If:

A = {pancakes, waffles, toast}
B = {bacon, sausage}

What is $A \cup B$?

Union Example

Given:

The alphabet $\{0,1\}$
$A = \{w \ |\ w$ begins with a 1$\}$
$B = \{w \ |\ w$ is even length$\}$

Can we build a DFA that recognizes $A \cup B$?

Regular Languages are Closed under Union

If $A_1$ and $A_2$ are regular languages, then so is $A_1 \cup A_2$.

To prove this, we use the following argument:

A regular language is one that a DFA can recognize.
We will assume $M_1$ is a DFA which recognizes $A_1$, and $M_2$ is a DFA which recognizes $A_2$.
We will build a DFA $M$ which recognizes $A_1 \cup A_2$ using $M_1$ and $M_2$.

$M$ will work by simulating both $M_1$ and $M_2$ at the same time:

The states of $M$ represent a pair of states: one from $M_1$ and one from $M_2$ (the cartesian product).
The alphabet is the union of the alphabets of $M_1$ and $M_2$.
The transition function calls the transition functions of $M_1$ and $M_2$ and joins the results to form the next state.
$q_0$ is the state comprised of the pair of $M_1$'s start state, and $M_2$'s start state.
$F$ is the set of states containing either a final state of $M_1$ or a final state of $M_2$.

For example, if $M_1$ is the following machine:

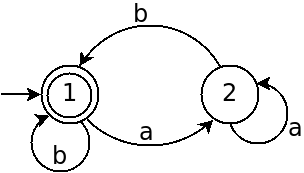
And $M_2$ is the following machine:

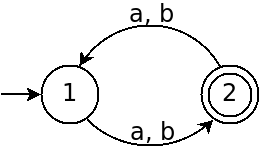
What is $A_1$?
What is $A_2$?
How can we construct the machine $M$ as above?

Intersection

$A \cap B = \{x \ |\ x \in A$ and $x \in B\}$

Are regular languages closed under intersection? How can we show it?

Concatenation

$A \circ B = \{xy \ |\ x \in A$ and $y \in B\}$

If:

A = {pancakes, waffles, toast}
B = {bacon, sausage}

What is $A \circ B$ ?

Star

$A \ast = \{x_{1}x_{2} ... x_{k} \ |\ k \geq 0$ and each $x_{i} \in A\}$

If:

A = {pancakes, waffles, toast}

What is $A\ast$?

Closure of Concatenation and Star

The class of regular languages are closed under both concatenation and star, but the proofs are difficult without non-determinism which we will look at next time.