Deterministic Finite Automata

Overview

DFAs are the simplest computational model we will consider. The "memory" of a DFA is limited to the state it is currently in. At each state, an input can move it into another state.

For example the following DFA accepts $.50 in exact change.

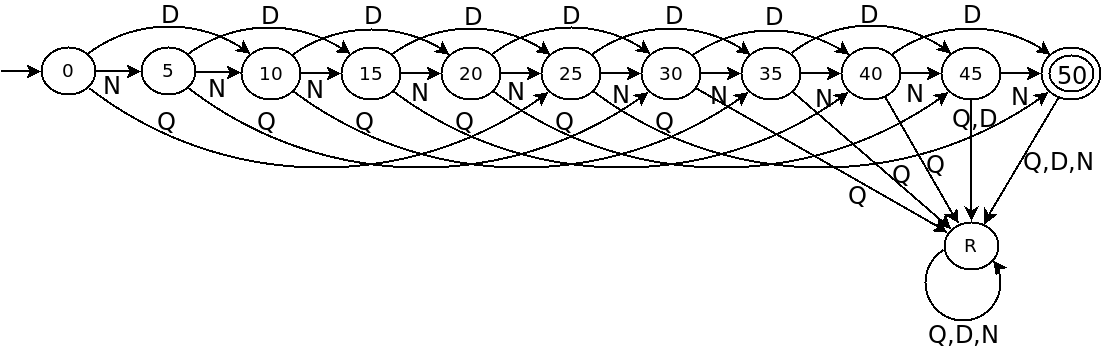
Note that:

The "start state" has an empty line entering it.
The "accept state" has a double circle.
The lines connecting states are "transitions" and are labeled with the input that moves us to another state.

The way that DFAs "compute" is by either accepting or rejecting their input according to their state rules.

DFA Definition

A DFA is composed by the following 5 things:

$Q$, the set of states.
$\Sigma$, the alphabet.
$\delta: Q \times \Sigma \rightarrow Q$, the transition function.
$q_0 \in Q$, the start state.
$F \subseteq Q$, the accept states.

For the example DFA above, we have:

$Q = \{0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, R\}$
$\Sigma = \{N, D, Q\}$
$\delta$ can be given as::

N D Q

0 5 10 25

5 10 15 30

10 15 20 35

15 20 25 40

20 25 30 45

25 30 35 50

30 35 40 R

35 40 45 R

40 45 50 R

45 50 R R

50 R R R

R R R R

Where the first column is the current state, and the next columns indicate which state to transition to with the given input.
$q_0 = 0$
$F = \{50\}$

Examples

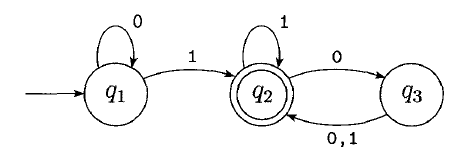
What is the formal definition of the following DFA?

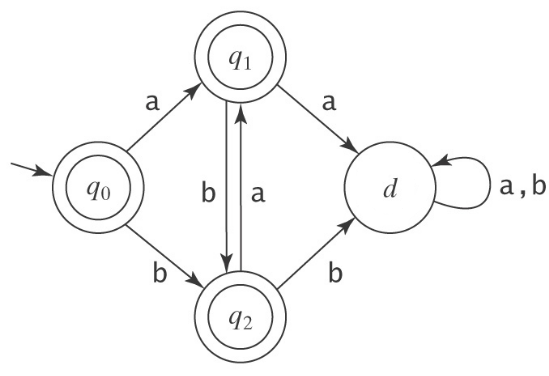
What about the following DFA?

Languages

We say that DFA $M$ accepts string $w$ iff $M$ ends up in an accept state when it has finished reading $w$.

We say that the language of $M$, written as $L(M)$ is the set of all strings denoted accepted by $M$. We also say that $L$ is recognized by $M$.

What is the language of the following DFA?

What about the following DFA?

Any language that is recognized by some DFA is said to be regular.

The Language of Floating Point Numbers

The language of floating-point numbers in typical programming languages is regular.

Examples:

33
3.0
+3.0
0.3E1
-3E+8
-33.33E-9

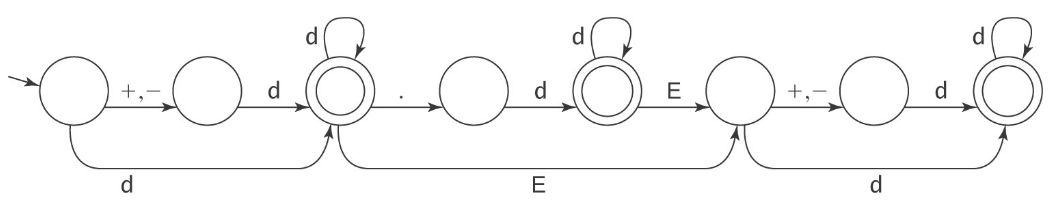
Here "d" refers to any digit 0-9

Compilers do in fact use finite automata for recognizing patterns like this.

	N	D	Q
0	5	10	25
5	10	15	30
10	15	20	35
15	20	25	40
20	25	30	45
25	30	35	50
30	35	40	R
35	40	45	R
40	45	50	R
45	50	R	R
50	R	R	R
R	R	R	R

	N	D	Q
0	5	10	25
5	10	15	30
10	15	20	35
15	20	25	40
20	25	30	45
25	30	35	50
30	35	40	R
35	40	45	R
40	45	50	R
45	50	R	R
50	R	R	R
R	R	R	R

	N	D	Q
0	5	10	25
5	10	15	30
10	15	20	35
15	20	25	40
20	25	30	45
25	30	35	50
30	35	40	R
35	40	45	R
40	45	50	R
45	50	R	R
50	R	R	R
R	R	R	R