Home CPSC 305

Carry Lookahead Adders

Ripple Carry

The simple adder constructed in Code is composed of a "half adder" which adds two bits into a sum and carry out:

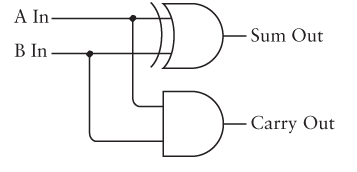
Two of these are then wired together to make a "full adder" which also takes into account an incoming carry:

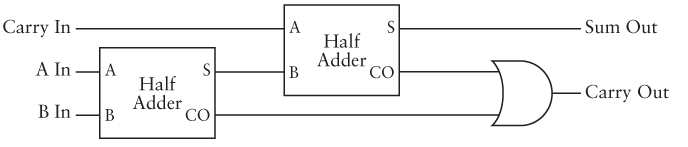
Then, multiple of these full adders are wired together to create a circuit which can add larger binary numbers:

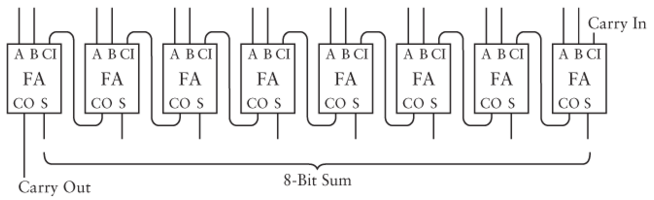
This circuit adds two eight bit numbers together, however it does not do so very efficiently. Remember that logic gates do not work instantaneously. If we change the input to a gate, there is some delay before the output changes.

For this adder to give us a full result, the carry has to propagate from the right-most full adder all the way to the left-most one. This type of adder is called a "ripple carry" adder for that reason.

A Logisim version of this adder is available at adder.circ.

The Importance of Adding

Adding is a hugely important operation. In addition to carrying out the additions that our programs specify, processors must also add for the following reasons:

Array access involves an addition, we need to add the index to the base address of the array.
Object field accesses involve an addition, we need to add the field offset to the base address of the object.
Most local variable accesses involve additions as well, of a stack offset to the base stack address.
Change of control instructions involve adding offsets to the current instruction address.
After every instruction, we need to add one to the current instruction address to go on to the next instruction.

Clearly addition is something we need to make as fast as possible!

Carry Lookahead Overview

The idea behind the carry lookahead adder (CLA) is that we don't just wait for the carries to ripple through the circuit. Instead we figure out ahead of time where the carries will come into play.

Consider the following truth table for the half adder above:

A	B	Carry-in	Carry-Out
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

If at least two of the inputs are 1, then carry out will be one as well. The following boolean expression produces carry-out:

$C_{out} = (A \ \&\ B) \ |\ ((A \oplus B) \ \ \&\ \ C_{in})$

The $(A \ \&\ B)$ part covers the last two rows of the truth table. If both inputs are 1, it does not matter if there is a carry in, there will be a carry out either way. We'll call this part a carry generator since it produces a "new" carry in the sum.

The $((A \oplus B) \ \ \&\ \ C_{in})$ part covers the other two cases. If exactly one of the inputs is 1 (given by $A \oplus B$), then only if there is a carry in, will there be a carry out. We'll call this a carry propagator since it passes an incoming carry along to the next part, but isn't creating one of its own. The $\oplus$ operator means XOR.

We'll define each piece separately to make talking about it easier:

$G = A \ \&\ B$

$P = A \oplus B$

$C_{out} = G \ |\ (P \ \ \&\ \ C_{in})$

$G$ will be true if the addition produces a new carry, and $P$ will be true if the addition will propagate a carry to the next addition. The CLA works by figuring out when carries will be produced and propagated ahead of time - before we actually know the value of C-in!

Carry Lookahead Calculations

Because there are multiple full adders in a complete adder (one for each bit of the inputs), then we can generalize the formula above for each of the adders:

$C_i = G_i \ |\ (P_i \ \&\ C_{i-1})$

Now we can write the specific formulas for the first two full adders:

$C_0 = G_0 \ |\ (P_0 \ \&\ C_{-1})$

$C_1 = G_1 \ |\ (P_1 \ \&\ C_{0})$

The first of these is OK in CLA because it does not require any carries to be calculated elsewhere - it only has the initial carry-in (if any) coming into it.

The formula for $C_1$ is a problem though, because it does depend on the carry calculated in the previous adder. To try and fix this, we will rewrite that expression, plugging in the value of $C_0$:

$C_1 = G_1 \ |\ \ (P_1 \ \&\ (G_0 \ |\ P_0 \ \&\ C_{-1}))$

The AND operator follows the same distributive property as the multiplication operator, as you can observer from the following table:

A	B	C	A & (B \| C)	(A & B) \| (A & C)
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
0	1	1	0	0
1	0	0	0	0
1	0	1	1	1
1	1	0	1	1
1	1	1	1	1

Because of this, we can simplify our equation above as:

$C_1 = G_1 \ |\ (P_1 \ \&\ G_0) \ |\ (P_1 \ \&\ P_0 \ \&\ C_{-1}))$

Now the computation of $C_1$ depends only on the initial values given to the adder, and not on any carries computed by previous full adders.

We can continue on for the formula giving $C_2$:

$C_2 = G_2 \ |\ (P_2 \ \&\ C_1)$

And then plug in the value of $C_1$ we got into the formula:

$C_2 = G_2 \ |\ (P_2 \ \&\ (G_1 \ |\ (P_1 \ \&\ G_0) \ |\ (P_1 \ \&\ P_0 \ \&\ C_{-1})))$

We can then simplify again which gives us this formula:

$C_2 = G_2 \ |\ (P_2 \ \&\ G_1) \ |\ (P_2 \ \&\ P_1 \ \&\ G_0) \ |\ (P_2 \ \&\ P_1 \ \&\ P_0 \ \&\ C_{-1})$

Skipping ahead, we can find that the formula for $C_3$ would be:

$C_3 = G_3 \ |\ (P_3 \ \&\ G_2) \ |\ (P_3 \ \&\ P_2 \ \&\ G_1) \ |\ (P_3 \ \&\ P_2 \ \&\ P_1 \ \&\ G_0) \ |\ (P_3 \ \&\ P_2 \ \&\ P_1 \ \&\ P_0 \ \&\ C_{-1})$

Carry Lookahead Operation

To summarize, this gives us the following way of calculating the carries for the first four bits of the addition:

$C_0 = G_0 \ |\ (P_0 \ \&\ C_{-1})$

$C_1 = G_1 \ |\ (P_1 \ \&\ G_0) \ |\ (P_1 \ \&\ P_0 \ \&\ C_{-1}))$

$C_2 = G_2 \ |\ (P_2 \ \&\ G_1) \ |\ (P_2 \ \&\ P_1 \ \&\ G_0) \ |\ (P_2 \ \&\ P_1 \ \&\ P_0 \ \&\ C_{-1})$

$C_3 = G_3 \ |\ (P_3 \ \&\ G_2) \ |\ (P_3 \ \&\ P_2 \ \&\ G_1) \ |\ (P_3 \ \&\ P_2 \ \&\ P_1 \ \&\ G_0) \ |\ (P_3 \ \&\ P_2 \ \&\ P_1 \ \&\ P_0 \ \&\ C_{-1})$

where

$G_i = A_i \ \&\ B_i$

$P_i = A_i \oplus B_i$

All of these input values are available as inputs into the adder, they do not rely on intermediate results (as the ripple carry adder does).

In the ripple carry adder, calculating the fourth carry takes twelve gate delays, because each full adder has two half-adders, and an OR gate, connected in serial, and the carry needs to propagate through four of them.

In the carry lookahead adder, despite there being many more gates, the fourth carry takes only three gate delays, because all of the values it takes one delay to calculate $G_i$ and $P_i$, another gate delay to AND the various values together, and a third to OR the results together.

Carry Lookahead Groups

Adders will generally not use carry lookahead for all of the bits of a sum. Instead, they will break the sum into several groups which use the carry lookahead method. The carries at the right end of each group are then propagated onto the next group using the normal ripple carry method.

This provides most of the speed of the carry lookahead method, but reduces the complexity of calculating the larger carries.

Below is a diagram of how we could create a carry lookahead group of size 4:

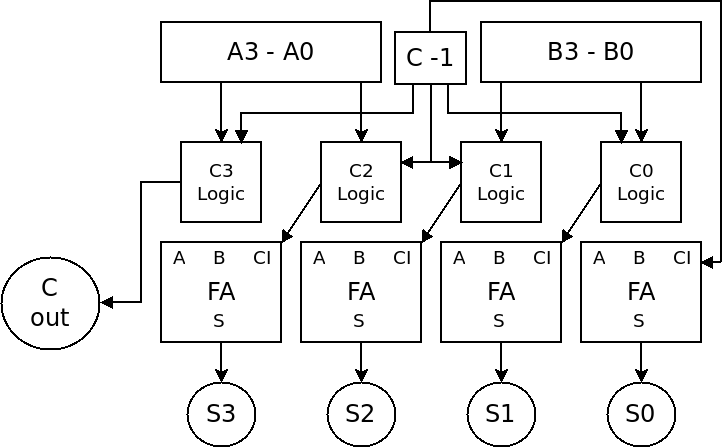
Here we have four full adders as described in Code, together with the four carry lookahead circuits we created above. All four of these adders are able to compute their sums in parallel, with no ripple of carry values. The final carry is the propagated to the next group.

If we combined 8 of these carry lookahead group circuits, we would have a 32-bit adder using carry lookahead to reduce the carry propagation from a factor of 32 to a factor of 8.

We could instead use 4 groups of size 8, which would be faster, but would result in a larger, more complex circuit, which would use more energy.

Conclusion

Some takeaways from the carry lookahead adder:

The carry lookahead adder is a faster circuit for adding binary numbers because it reduces the propagation time of carry values.
Doing more work does not necessarily make a circuit slower. Circuits are inherently parallel, and you only count serial operations when discussing speed.
Designing circuits involves trade-offs among speed, complexity, size and power.