
Last time we talked about decidable problems relating to finite automata and context-free grammars. Today we will look at equivalent problems concerning Turing machines and see that they do not have solutions.
The TM acceptance problem is stated as:
$A_{TM} = \{ \langle M, w\rangle\; |\; M \text{ is a Turing machine that accepts } w\}$.
This problem is not decidable, but it is Turing recognizable. What algorithm could we write that would recognize this language?
In order to prove that $A_{TM}$ is not decidable, we will need to use a diagonalization argument.
Diagonalization is a technique proposed by Georg Cantor who was concerned with the sizes of infinite sets. Cantor proposed that two sets are of equal size if elements in each set can be paired together.
If there is a function that maps the elements of set $A$ to elements of set $B$, such that it maps each element of $A$ to a different element in $B$, and every element in $B$ is accounted for, then the function provides a correspondence.
For example, there is a correspondence between even numbers, $\mathcal E$ and natural numbers, $\mathcal N$:
| $\mathcal N$ | $\mathcal E$ |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| ... | ... |
Here the correspondence is simply $f(n) = 2n$.
We say that a set is countable if it has a correspondence with the natural numbers.
Another countable set is the rational numbers, $\mathcal Q$. The correspondence orders them in the following pattern:
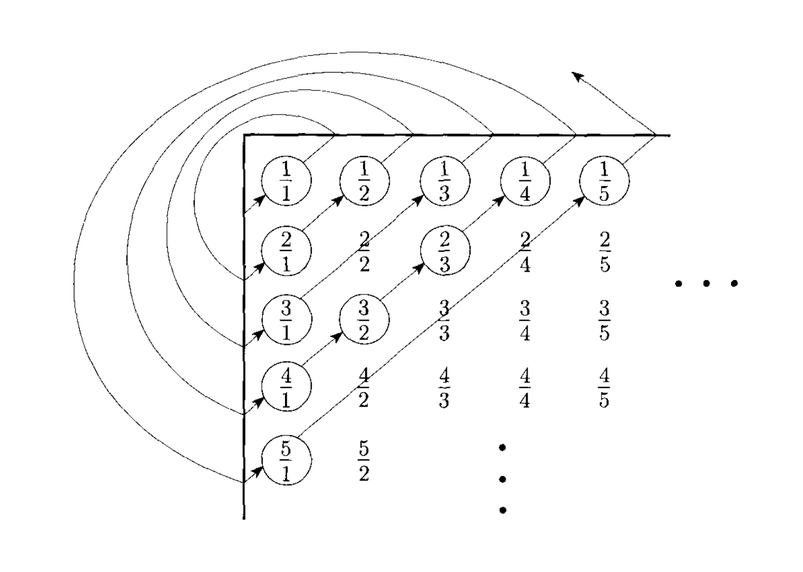
On the other hand, the set of real numbers, $\mathcal R$ is uncountable: it has no correspondence with $\mathcal N$. To show this, suppose there was a correspondence between $\mathcal N$ and $\mathcal R$:
| $\mathcal N$ | $\mathcal R$ |
| 1 | 3.14159... |
| 2 | 55.1555... |
| 3 | 0.12345... |
| 4 | 0.50000... |
| ... | ... |
Given a potential correspondence, we can construct a number $x$ that exists in $\mathcal R$ that has no entry in the table.
To ensure $f(1) \ne x$, we let the first digit of $x$ be anything other than the first digit of $f(1)$. Likewise, we pick the second digit of $x$ to be anything but the second digit of $f(2)$ and so on.
This allows us to build a number $x$ which cannot possibly appear in the correspondence with $\mathcal N$. Therefore $\mathcal R$ is not countable. This is a diagonalization argument.
$A_{TM} = \{ \langle M, w\rangle\; |\; M \text{ is a Turing machine that accepts } w\}$.
First, we assume that $A_{TM}$ is decidable, in order to obtain a contradiction. If $A_{TM}$ is decidable, there is some Turing machine, $H$ decides it.
$H(\langle M, w \rangle)$ will accept if $M$ accepts $w$ and reject if $M$ does not accept $w$ (either by rejecting or looping indefinitely).
We can then use $H$ to build a Turing machine $D$:
$D = $ "On input $\langle M \rangle$, where $M$ is a Turing machine:
The Turing machine $D$ takes a Turing machine $M$ as input, then runs the Turing machine $H$ to see if $M$ accepts its own description. If $M$ accepts itself, then $D$ rejects, and vice versa.
If we run $D$ on itself, then $D$ will run itself on its own description. If $D$ accepts itself, then $D$ must reject. Otherwise, if $D$ rejects itself, then $D$ must accept.
Because this is a contradiction, $D$ and $H$ cannot exist. Because $H$ cannot exist, $A_{TM}$ must not be decidable.
This can also be viewed as a diagonalization argument. If we list all possible Turing machines along with their descriptions in a table:

Then we essentially construct the Turing machine $D$ to do the opposite of the diagonal entries:
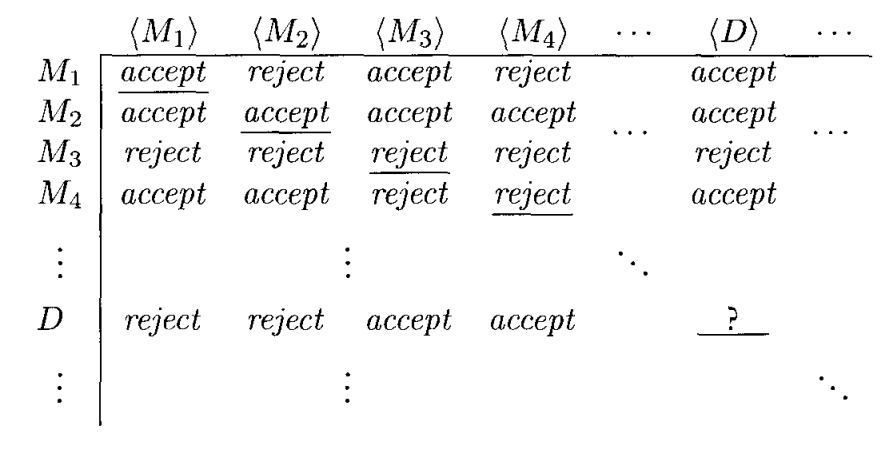
Which leads to the contradiction.
Reducibility refers to the act of using the solution to one problem as a means to solve another.
For example, the problem of finding the area of a rectangle reduces to the problem of multiplying the length of the rectangle by the width of the rectangle.
A reduction involves two problems, $A$ and $B$. If we can show that $A$ reduces to $B$, then we can use a solution to $B$ to produce solutions to $A$.
In this class we will use reductions in the following arguments.
The halting problem can be stated as:
$HALT_{TM} = \{\langle M, w \rangle\; |\; M \; \text{is a TM which halts on input }w\}$.
Given some Turing machine, and some input, we would like to say whether or not the Turing machine will halt on that input.
This would be a very nice algorithm to have, as it could let us avoid infinite loops in our programs.
Unfortunately, $HALT_{TM}$ is undecidable according to the following proof by contradiction:
Assume $HALT_{TM}$ is decidable. This means there would exist a Turing machine, $R$, which decides $HALT_{TM}$. We can then use this Turing machine to build a Turing machine $S$ which decides $A_{TM}$:
$S = $"On input $\langle M, w \rangle$:
Because we have already shown $A_{TM}$ to be undecidable, the machine $S$ cannot exist, and therefore neither can $R$. Because no decider can exist for $HALT_{TM}$, it must be undecidable.
The reduction here is that $A_{TM}$ reduces to $HALT_{TM}$. Because $A_{TM}$ is undecidable, so is $HALT_{TM}$.
The emptiness problem for Turing machines is stated as:
$E_{TM} = \{\langle M\rangle\; |\; M \text{ is a TM and } L(M) = \emptyset\}$.
We can also show that $E_{TM}$ is undecidable by reducing $A_{TM}$ to $E_{TM}$, but doing so is not as obvious.
To do so, we again assume that $E_{TM}$ is decidable and that some Turing machine, $R$ decides it.
We then want to construct a Turing machine $S$ that takes a machine $M$ and a string $w$ and decides whether or not $M$ accepts $w$.
If we run $R$ on $M$, and $R$ accepts, then we can have $S$ reject (because $M$ is empty and will not accept $w$). However, if $R$ rejects, then we know $M$ accepts some strings, but don't know if that includes $w$ or not.
Instead, we will have $S$ build a new Turing machine $M_1$ that rejects all strings that are not equal to $w$, and accepts $w$ if and only if $M$ does.
The full Turing machine is as follows:
$S =$ "On input $\langle M, w \rangle$:
Construct a Turing machine $M_1$ from $M$:
$M_1 =$ "On input $x$:
We specifically build $M_1$ to only accept $w$ if $M$ accepts $w$, and accept zero strings if $M$ does not accept $w$. We then test if $M_1$ is empty which will tell us whether or not $M$ accepts $w$ or not. Note that we never actually run $M_1$ in this algorithm, we just examine it to see if it's empty.
Because this algorithm uses a decider of $E_{TM}$ to decide $A_{TM}$, and we know that $A_{TM}$ is undecidable, $E_{TM}$ must be undecidable as well.
This problem can be stated as:
$EQ_{TM} = \{\langle M_1, M_2 \rangle\; |\; M_1 \text{ and } M_2 \text{ are Turing machines and } L(M_1) = L(M_2)\}$.
Given two Turing machines, can we determine if they accept the same languages?
This problem is undecidable. To show this, we can reduce the $E_{TM}$ problem to $EQ_{TM}$. Recall that $E_{TM}$ is the problem of determining whether the language of a given Turing machine is $\emptyset$ (i.e. the Turing machine accepts no strings). Also recall that $E_{TM}$ is undecidable.
We will begin by assuming that $EQ_{TM}$ is decidable and some Turing machine $R$ decides it.
$S =$ "On input $\langle M\rangle$ where $M$ is a Turing machine:
If we could decide if two Turing machines were equivalent, then we could use that to decide if a particular Turing machine is equivalent to an empty Turing machine. This would decide $E_{TM}$ which we know is undecidable.
Therefore, there is no machine $R$ that decides $EQ_{TM}$ which is undecidable.
This problem can be stated as:
$REGULAR_{TM} = \{\langle M \rangle\; |\; M \text{ is a Turing machine, and } L(M) \text{ is a regular language}\}.$
Given some Turing machine, can we determine whether a DFA could compute the same language as the Turing machine?
No, this language is also undecidable. To show this, we will again assume that $REGULAR_{TM}$ is decidable and that some Turing machine, $R$ decides it.
We then want to construct a Turing machine $S$ that uses $R$ to decide $A_{TM}$. We will then conclude that, because $A_{TM}$ is undecidable, and $R$ allows us to decide it, the machine $R$ cannot exist, so $REGULAR_{TM}$ must be undecidable.
The difficulty is in building $S$ from $R$.
To do this, we will again have the machine $S$ construct a Turing machine $M_1$. The goal of $M_1$ is to accept either the language $\{0^n1^n\}$ (a non-regular language), or all strings (a regular language) - based on running $M$ on $w$.
The full definition of $S$ is:
$S = \text{"On input } \langle M, w\rangle \text{ where } M \text{ is a Turing machine, and } w \text{ is a stinrg:}$
$M_1 = \text{"On input } x$:
The following table gives the possibilities of running $M$ on $w$. $M_1$ is designed such that it accepts a regular language iff $M$ accepts $w$.
| Running $M$ on $w$ | Language accepted by $M_1$ | Output of $S$ |
| Accept | $\Sigma^\ast$ (regular) | Accept |
| Reject | $0^n1^n$ (non-regular) | Reject |
| Loop | $0^n1^n$ (non-regular) | Reject |
Note that the use of $0^n1^n$ is arbitrary. We could use any non-regular language instead.
Also note that we never actually run $M_1$. The fact that it could infinite loop on some inputs does not matter. If we had a decider to tell us if $M_1$ is regular, we could use it to decide $A_{TM}$.
Because we know this to be impossible, $R$ cannot exist, so $REGULAR_{TM}$ is undecidable.
Note that the above proof could be used to show that $CF_{TM}$ - the problem of determining whether a language is context-free is also undecidable. We could simply replace $0^n1^n$ with a language that was not context-free such as $a^nb^nc^n$.
The generalization of these results is called Rice's theorem which says that determining any non-trivial property of the language accepted by a Turing machine is undecidable.
Computers are so powerful it may seem any problem could be solved with a program. These results show that this is not the case. There are problems beyond the scope of any computer.
Knowing this, and having an insight into what types of problems are computable and which aren't is important.
Copyright © 2024 Ian Finlayson | Licensed under a Attribution-NonCommercial 4.0 International License.