
Computer circuits are built out of simple transistors, but computer designers don't often deal with transistors directly. Instead, they use higher level structures built from transistors. The simplest of these are the gates.
Logic gates implement simple boolean functions with transistors.
Below are truth tables and the diagrams used for each of the seven most common logic gates.
and
|

|
or
|
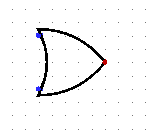
|
not
|
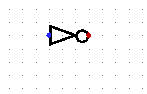
|
nor
|
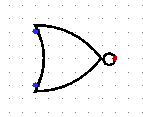
|
nand
|
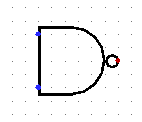
|
xor
|
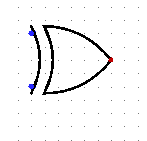
|
xnor
|
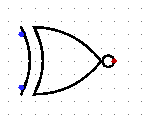
|
How could each of these be implemented with transistors?
We actually don't need all seven logic gates to build circuits. We can in fact build all of the other gates using just AND and NOT, or just OR and NOT
How could we build an OR gate using AND and NOT gates?
How could we build an AND gate using OR and NOT gates?
There are actually two gates which are "universal" in that they alone can be used to build any of the other gates, and in fact any logical function whatsoever. Those two gates are NAND and NOR.
The construction of the other gates out of NAND and NOR is slightly more complicated than the two examples above, but the constructions are given in the Wikipedia articles on NAND Logic and NOR Logic.
Because NAND and NOR are universal, they are often used to implement entire circuits. Either type of gate could be used to build any piece of circuitry we could want.
NAND gates are actually preferred because they can be made to be faster than NOR gates. A NAND gate can be constructed from two P-type transistors in parallel:
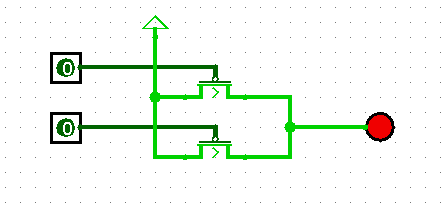
A NOR gate can be constructed from two P-type transistors in sequence:
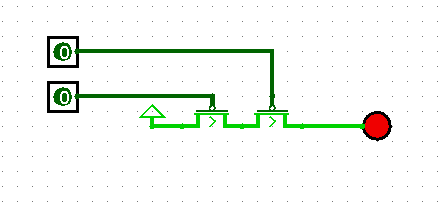
NAND gates switch faster than NOR gates, because the time for the entire gate is the time for one transistor to switch. With the NOR gate, the time taken is the time for two transistors to switch, one after the other.
NAND gates are the most widely used because they are universal, only require two transistors, and switch quickly.
However, designers don't need to think in terms of NAND gates directly. As we will see, there are tools which can take logical expressions and "compile" them into circuits which use only NAND.
Copyright © 2024 Ian Finlayson | Licensed under a Attribution-NonCommercial 4.0 International License.